

Zum einen sind es physikalische Theorien und zum anderen sind es Dinge, die von diesen nicht erklärt werden können.
Das dabei vielleicht am unwichtigsten Erscheinende sind wohl die Bahnstrukturen der Planeten. Ganz abgesehen davon, dass dieser Frage seit etwa 400 Jahren hin und wieder nachgegangen wurde, gilt heute, von bedeutenden Theoretikern vertreten, die Meinung, diese Frage sei nicht relevant, da die Bahnparameter von Planetenbahnen bis auf das, was die Keplerschen Gesetze hergeben, historischer Zufall sei.
Wenn das nun aber ein Irrtum ist und zukünftig zu erwartende immer genauere astronomische Ergebnisse auf etwas anderes hindeuten?
Dann wird man sich dieser Frage widmen müssen und wird, vielleicht mathematisch auf anderen Wegen, bei einer zur oben erwähnten, von mir Makroquantenphysik (MQT) getauften, äquvalenten Theorie landen. Denn diese Theorie ist neu und sie lässt sich mathematisch im Gegensatz zu anderen aufgestellten oder postulierten Theorien aus der klassischen Mechanik exakt herleiten. Sie löst das Problem der Bahndaten, das ich "Keplerproblem" genannt habe, weil sich Johannes Kepler nachweislich, wenn auch erfolglos, bereits zu Anfang des 17. Jahrhunderts um eine Lösung bemüht hat.
Und darüber hinaus ist diese neue Theorie im notwendigen Einklang zu allen etablierten Theorien der Theoretischen Physik nicht nur die Lösung des Keplerproblems, sondern sie ist auch eine Art Schlüsselfunktion, die zu den anderen oben genannten offenen Problemen wie Dunkle Materie, Dunkle Energie, Quantengravitation und schließlich der Frage, was es denn mit der Feinstrukturkonstanten in ihrer eigentlichen physikalischen Bedeutung auf sich hat, zumindest erste Antworten gibt.
Anmerkung: Es ist aber möglich, dass eine Theorie richtig ist und Vorhersagen nicht nachweisbar sind, weil sie außerhalb der technischen Möglichkeiten liegen. Das gleiche gilt für die Widerlegbarkeit. Die Bestätigung von Aussagen wird immer nur mit einer Wahrscheinlichkeit möglich sein, deshalb müssen Überlegungen zur Aussagesicherheit angestellt werden, um nicht Zufälligkeiten zu erliegen. Dem wird im nächsten Abschnitt nachgegangen.
Ob durch Experiment oder Beobachtung - es entstehen immer Ergebnisse in Form von Daten. Diese aber sind stets mehr oder weniger fehlerbehaftet. Deshalb ist es notwendig, zu prüfen, mit welcher Wahrscheinlichkeit es sich um Zufall oder einen wie auch immer gesicherten brauchbaren Wert handelt. Es ist also die Frage, wird eine Theorie durch belastbare Werte bestätigt oder beruht sie auf einer Art "Zahlenmystik".
Die Zahl 137 gilt nicht nur unter Esoterikern, sondern auch unter bedeutenden Wissenschaftlern wie zum Beipiel Richard Feynman oder Wolfgang Pauli als mystische Zahl, das kann man unschwer im Internet recherchieren (z.B. www.futurezone.de). Sie ist als natürliche Zahl dem reziproken Wert der Feinstrukturkonstanten am nächsten. Letztere aber gilt als wichtige und zugleich Geheimnis umwitterte Größe in der Physik und wurde zuerst von Arnold Sommerfeld 1916 entdeckt.
Dabei ist sie "nur" eine Verhältniszahl zwischen der elektrostatischen Elementarkraft (Coulombkraft) zweier Elementarladungen zu einer maximal möglichen durch Lichtgeschwindigkeit und Plancksches Wirkungsquantum begrenzten absoluten Grenzkraft, die sich aus den bereits 1906 von Max Planck beschriebenen Planck-Einheiten", Darstellungen aller physikalischen Größen aus Naturkonstanten, ableiten lässt.
Sie ist also kein Mysterium, sondern eine einfache Verhältniszahl zwischen zwei, wenn auch wichtigen physikalischen Kräften und damit vergleichbar der Ludolfschen Zahl "π".

Fazit: Was rätselhaft erscheint, kann einfach, logisch und bedeutend sein. Die veröffentlichte Begründung ist unter "Bedeutung der Feinstrukturkonstanten" nachzulesen.
Lotto 6 aus 49 kennen wohl die meisten. Die Wahrscheinlichkeit, mit einem einzigen Lottoschein einen "Sechser" zu landen, wohl oft nicht. Sie ist 1 : 13.983.816 - nicht gerade sehr hoch.
Angenommen, es käme jemand zu Ihnen und behauptete, er hätte eine "todsichere" Methode, einen solchen Gewinn zu machen, brauchte aber für sein System unbedingt Lottoscheine im Wert von 1000 € und hätte selbst leider nur 500 €, ob Sie mitmachten, das Risiko, aber auch den "sicheren" Gewinn mit ihm teilten und die restlichen 500 € dafür einsetzen würden. Was würden Sie tun?
Statistisch gesehen ist das für mich klar. Die Zahlenziehung erfolgt nach einem Zufallsprinzip, d. h. um mit guter Sicherheit zu gewinnen, müsste das für mehr als 13900 Ziehungen, also ein Leben lang, durchgehalten werden und würde mich erst einmal einige Mio. € kosten.
Wenn ich die hätte, machte ich mir kaum die Mühe mit der Lotterie, um am Ende die Differenz zwischen Gewinn und Kosten zu haben, die auch negativ sein könnte.
Was aber, wenn derjenige doch ein sicheres System besitzt? An Wunder zu glauben, ist gefährlich.
Fazit: Ohne Kenntnis der Aussagesicherheit sind Aussagen mit Vorsicht zu genießen!
Nehmen wir an, Sie haben eine Idee, eine Vorstellung oder eine Theorie über ein System und wollen den Zustand des Systems daraufhin überprüfen. Auch die Prüfmethode dafür haben Sie und können damit die folgenden Messwerte erzielen:
0.3074
0.4666
0.9833
1.016
1.666
29.659
49.305
Mit Ihrer Untersuchungsmethode können Sie eine Genauigkeit garantieren, die die Werte wie angegeben zulässt.
Nun wollen Sie wissen, ob die Ergebnisse zufälligen Charakter haben, oder ob eine Aussage darin verborgen ist, vielleicht sogar ein physikalischer Zusammenhang. Wie kann man aus diesen Zahlen eine Aussage gewinnen, die jeden Zufall ausschließt, ist also die Frage. Nach langen Überlegungen und angeregt durch die Werte selbst, kommen Sie auf die Idee, die Werte der Messergebnisse etwas anders darzustellen.
| 20/60 - 2/60 | = 0.3000 |
| 30/60 - 2/60 | = 0.4667 |
| 60/60 - 1/60 | = 0.9833 |
| 60/60 + 1/60 | = 1.0160 |
| 100/60 | = 1.6670 |
| 1800/60 | = 30.00 |
| 3000/60 | = 50.00 |
Jetzt ist eine Struktur zu erkennen. Fünf Werte werden damit sehr gut wiedergegeben, die anderen einigermaßen. Offensichtlich gibt es eine Gemeinsamkeit für alle Werte, die Zahl 60 im Nenner und Laufwerte im Zähler, sowie Korrekturwerte für die ersten vier.
Aber selbst, wenn man nun vielleicht eine mehr oder weniger komplizierte mathematische Reihe oder besser Zahlenfolge bilden würde, die gewünschte Aussage bekommt man damit nicht. Denn Zahlenfolgen oder -reihen, falls sie sich einfach bilden lassen, bieten nur eine Vereinfachung. Eine Aussage, ob Ihr System in Ihrer Modellvorstellung dafür verantwortlich ist, demnach ein möglichst physikalisch sinnvoller Zusammenhang besteht, liefert dieser Weg nicht.
Aber haben Sie für Ihr System eine Modellvorstellung und eine mathematische Formulierung, so sollte es Lösungen geben, die nicht nur zu besseren Ergebnissen, sondern auch zur gewünschten Aussage führen. Sie suchen also erst einmal nach mathematischen Lösungen zu ihrem Modell oder Ihrer Theorie, ohne auf die Messergebnisse zu achten, und erhalten zum Beispiel als Lösung die folgende Formel:
Wert (n, m, l ) = (n/m) πl mit "n, m und l" als natürlichen Zahlen.
Diese Formel sollte also die richtigen Werte liefern und wir stellen ihre Werte in der nächsten Tabelle zusammen.
Sie enthält aber zugleich weitere Informationen, die in der Tabelle bestätigt werden. Der Zähler "n" ist tatsächlich ein Zählindex, während "l" im Zusammenspiel mit "π" ein Gruppenmerkmal ist, denn es trennt für "l = 0" rationale Werte von ansonsten irrationalen.
Tabelle der bisher betrachteten Werte:
| n | m | l | Wert THEO | Wert GEM | Delta (abs) | Korr. mit i/60 | Wert NEU | Delta |
|---|---|---|---|---|---|---|---|---|
| 2 | 6 | 0 | 0.3333 | 0.3074 | 0.0259 | 8.43 % | -2 | 0.3000 | 0.0074 | 2.41 % |
| 3 | 6 | 0 | 0.5000 | 0.4667 | 0.0333 | 7.14 % | -2 | 0.4667 | 0.0000 | 0.00 % |
| 6 | 6 | 0 | 1.0000 | 0.9833 | 0.0167 | 1.70 % | -1 | 0.9833 | 0.0000 | 0.00 % |
| 6 | 6 | 0 | 1.0000 | 1.0167 | 0.0167 | 1.64 % | +1 | 1.0167 | 0.0000 | 0.00 % |
| 10 | 6 | 0 | 1.6667 | 1.6667 | 0.0000 | 0.00 % | 0 | 1.6667 | 0.0000 | 0.00 % |
| 3 | 1 | 2 | 29.6090 | 29.659 | 0.0500 | 0.19 % | +3 | 29.659 | 0.0000 | 0.00 % |
| 5 | 1 | 2 | 49.3480 | 49.305 | 0.0430 | 0.09 % | 0 | 49.348 | 0.0430 | 0.09 % |
Unschwer ist in der Tabelle sowohl die Zähleigenschaft von "n" als auch die Gruppierung durch "m" und "l" zu erkennen. Und auch die Wirkung der schon weiter oben angeführten Korrektur, die auf eine einheitliche Störgröße (mit dem Wert 60) in der einen Gruppe mit unterschiedlicher, aber durch "i" zählbaren Einwirkung hindeutet.
Der Zähler "n" hat aber Lücken in der Gruppe "m = 6 und l = 0 für n = 1, 4, 5, 7-9" und der Gruppe "m = 1 und l = 2 für n = 1, 2 und 4", was als Voraussage gedeutet werden kann, nämlich, dass an den Fehlstellen nach weiteren Werten im analysierten System gesucht werden sollte.
Also suchten wir erneut und fänden tatsächlich die Werte:
0.7233
1.3815
1.5240
5.203
9.5826
19.2010
39.4800
und trotz mehrmaliger Überprüfung weiter keine.
Wir erstellen eine Ergänzungstabelle nach obigem Schema und versuchen die Werte einzuordnen:
| n | m | l | Wert THEO | Wert GEM | Delta (abs) | Korr. mit i/60 | Wert NEU | Delta |
|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 0 | 0.1667 | ? | ||||
| 4 | 6 | 0 | 0.6667 | 0.7233 | 0.0566 | 7.38 % | + 3 | 0.7167 | 0.0066 | 0.91% |
| 5 | 6 | 0 | 0.8333 | ? | ||||
| 7 | 6 | 0 | 1.1667 | ? | ||||
| 8 | 6 | 0 | 1.3333 | 1.3815 | 0.0482 | 3.49 % | + 3 | 1.3833 | 0.0018 | 0.13 % |
| 9 | 6 | 0 | 1.5000 | 1.5240 | 0.0240 | 1.57% | + 2 | 1.5333 | 0.0093 | 0.61 % |
| 1 | 2 | 2 | 4.9348 | 5.2030 | 0.2682 | 5.15 % | +16 | 5.2015 | 0.0015 | 0.03 % |
| 1 | 1 | 2 | 9.8696 | 9.5826 | 0.2870 | 3.00 % | -20 | 9.5359 | 0.0467 | 0.49 % |
| 2 | 1 | 2 | 19.7390 | 19.201 | 0.5382 | 2.80 % | -30 | 19.2392 | 0.0382 | 0.02 % |
| 4 | 1 | 2 | 39.4780 | 39.482 | 0.0040 | 0.00 % | 0 | 39.478 | 0.0040 | 0.00 % |
Ein Wert (rot) passt zwar in die Tabelle, scheint aber in seiner Gruppe mit "m = 2" eine Art Untergruppe zu bilden.
In der Gruppe "m = 1 und l = 2" werden alle Zähler n = 1 - 5" lückenlos belegt. In der Gruppe "m = 6 und l = 0" aber bleiben Lücken. Was kann man daraus schließen? Meine Meinung ist, da fehlt etwas, ist verloren gegangen oder hat nie existiert.
Was Sie glauben, überlasse ich Ihnen. Offen ist ja noch die Frage, ist das Zahlenspielerei, Zahlenmystik oder beweisen diese Werte etwas? Wir hatten doch wohl eine Theorie, sonst wären wir nicht zur Formel gelangt und wollen nun wissen, widersprechen die gemessenen der Theorie, bzw. mit welcher Sicherheit bestätigen sie diese. Da man Theorien nicht beweisen kann, versuchen wir die These, dass die Messwerte mit den theoretisch erwarteten übereinstimmen, zu widerlegen.
Die Frage lautet also, mit welcher Wahrscheinlichkeit stimmen die gemessenen nicht mit den berechneten Werten überein.
Die Werte müssen, wenn sie übereinstimmen, der Gleichung f(x) = y = x genügen. Setzen wir die gemessenen Werte als "y" und die nach der Formel berechneten als "x" an, so sollten sie möglichst genau auf der 45-Grad-Geraden liegen und wir können die den Werte-Paaren zugrunde liegende Geradengleichung mit Hilfe der linearen Regression bestimmen. Dann sind wir der gesuchten Aussagesicherheit ein ganzes Stück näher, denn der Anstieg der Geraden sollte ja 45 Grad betragen und ihr Vertrauensbereich (Konfidenzintervall) darf bei der gesuchten Sicherheit gerade noch nicht gleich Null, also waagerecht sein. Die nahe beim Anstieg "Null" liegende Wahrscheinlichkeit ist unsere gesuchte Aussagesicherheit dafür, dass Theorie und Messung sich nicht widersprechen.
Ohne auf das rechnerische Verfahren weiter einzugehen, führen wir die Regressionen der Werte beider Tabellen einmal ohne und einmal mit Korrektur durch und beschränken uns auf eine Aussagesicherheit von 99.95 %.
Im Vergleich die korrigierten Werte zu den unkorrigierten und das sowohl für eine lineare als auch doppeltlogarithmische Regression, die bei stark auseinanderliegenden Werten realistischere Aussagen bringt. Im Vergleich dazu wie die Aussagen sich verändern, wenn man nur eine spezielle Gruppe von Daten berücksichtigt und auch ein Vergleich als Beispiel wie das mit Planetendaten bei der Titius-Bode-Reihe nach Einführung der astronomischen Einheit durch Johann Friedrich Wurm 1787 (hier nur linear) bei ihrer Aufstellung, nach Entdeckung des Uranus und der Asteroiden sowie nach Entdeckung der Planeten Neptun und Pluto ausgegangen wäre.
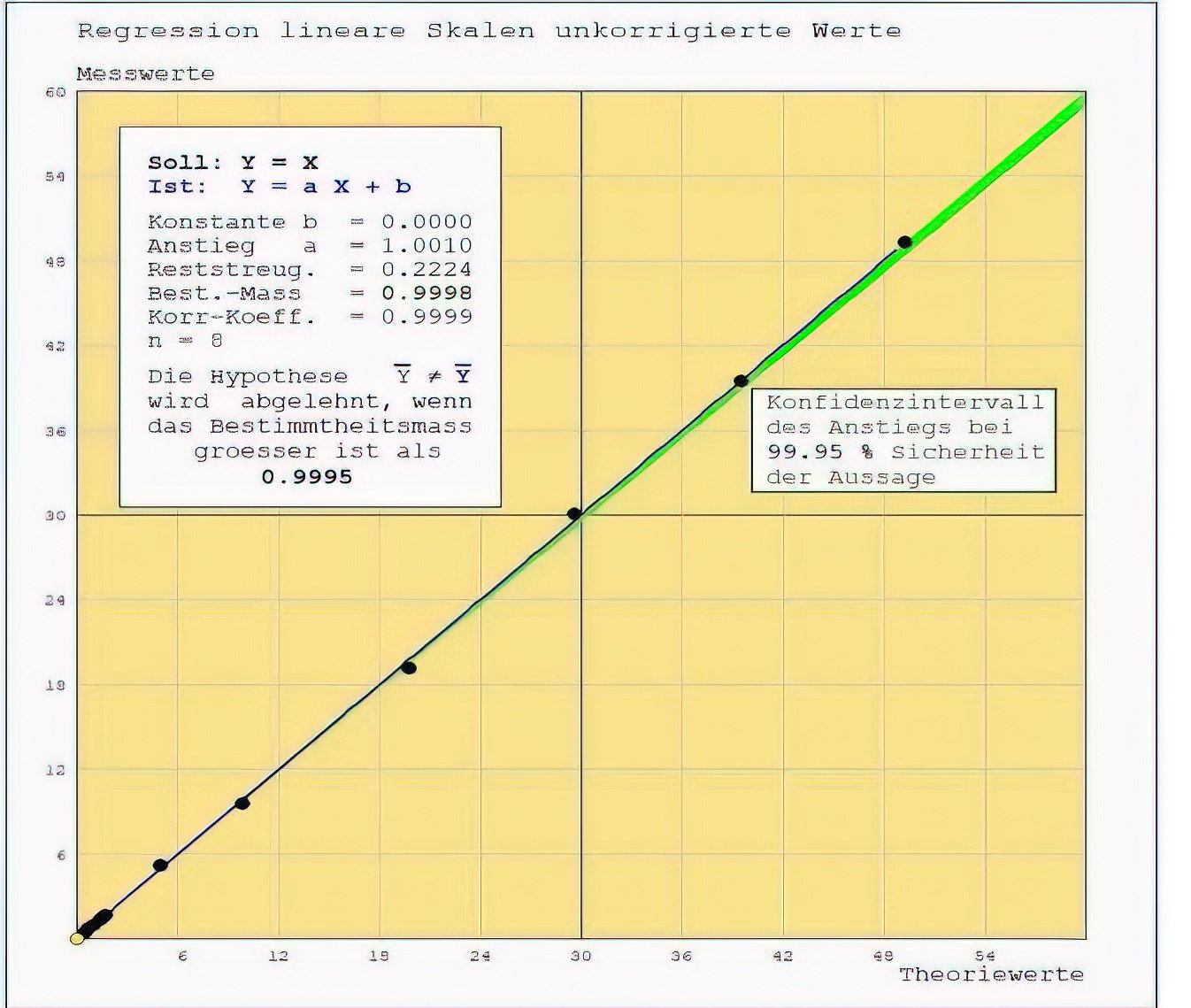
Hier sind alle Daten verwendet. Das Konfidenzintervall des Anstiegs bei 99.95% Sicherheit ist extrem schmal, obwohl die kleinen Werte nur als einer gezählt werden und deutet darauf hin, dass der Anstieg als Kriterium für die Hypothese, ab wann die Aussage "Theorie = Messdaten" abgelehnt werden muss, unzureichend ist. Ursache ist die extreme Aufspreizung der Daten.
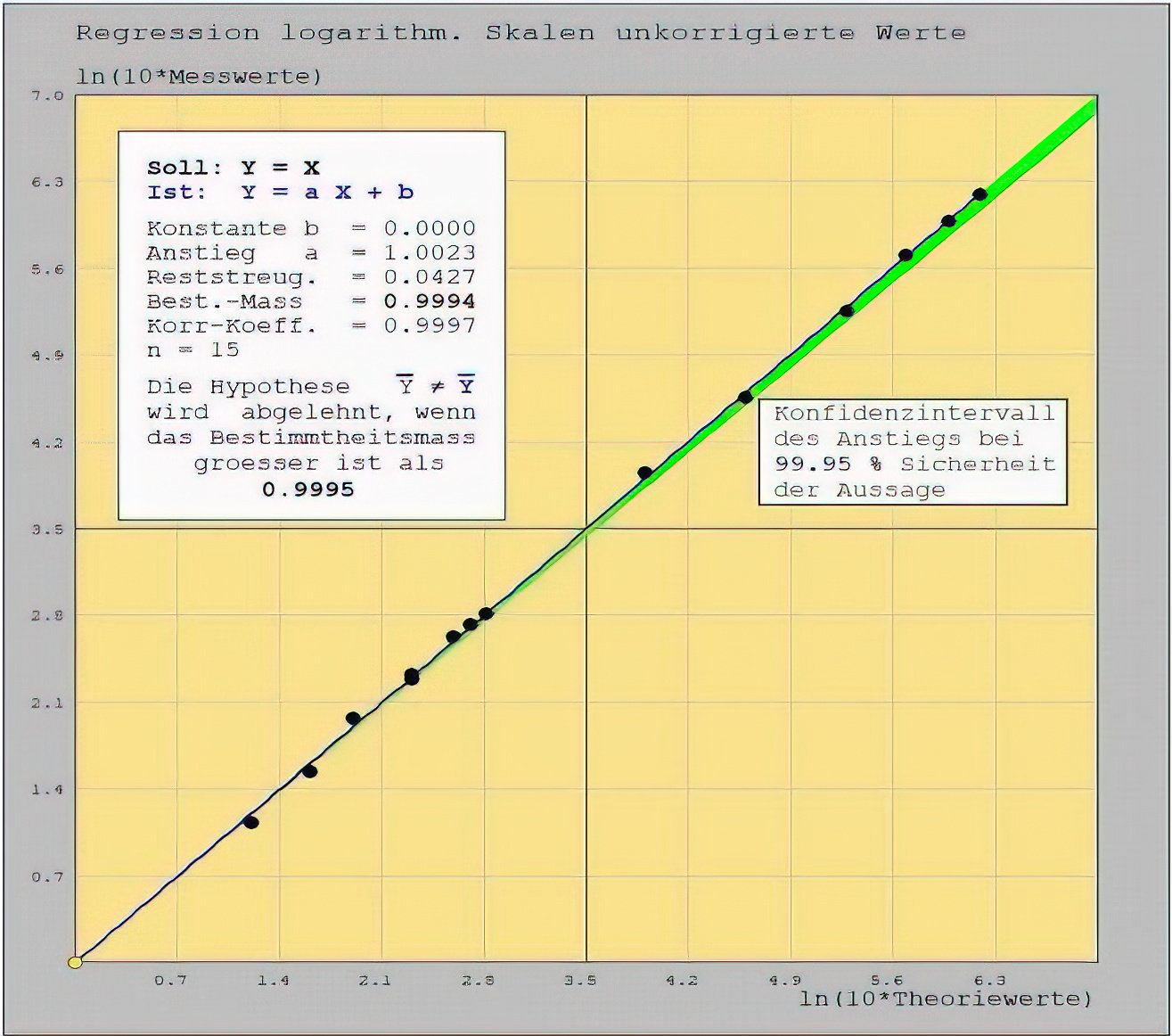
In logarithmischen Skalen ist die Aufspreizung stark reduziert. Das Konfidenzintervall des Anstiegs bleibt extrem schmal und ist auch hier für die Aussage ungeeignet. Das Bestimmtheitsmaß jedoch unterschreitet gering die vorgegebene Schranke von 0,9995 - wirkt also stark und scheint als Kriterium geeignet.
Die unkorrigierten Theoriedaten werden zur Bestätigung, dass die Messwerte die Theorie repräsentieren, gerade noch abgelehnt.

Nutzt man die korrigierten Daten, so wird die These nicht mehr abgelehnt, dass die Messdaten die Theorie bestätigen. Das Bestimmtheitsmaß sagt also aus. die Korrektur entscheidet die Frage, "Theorie = Praxis" oder nicht.
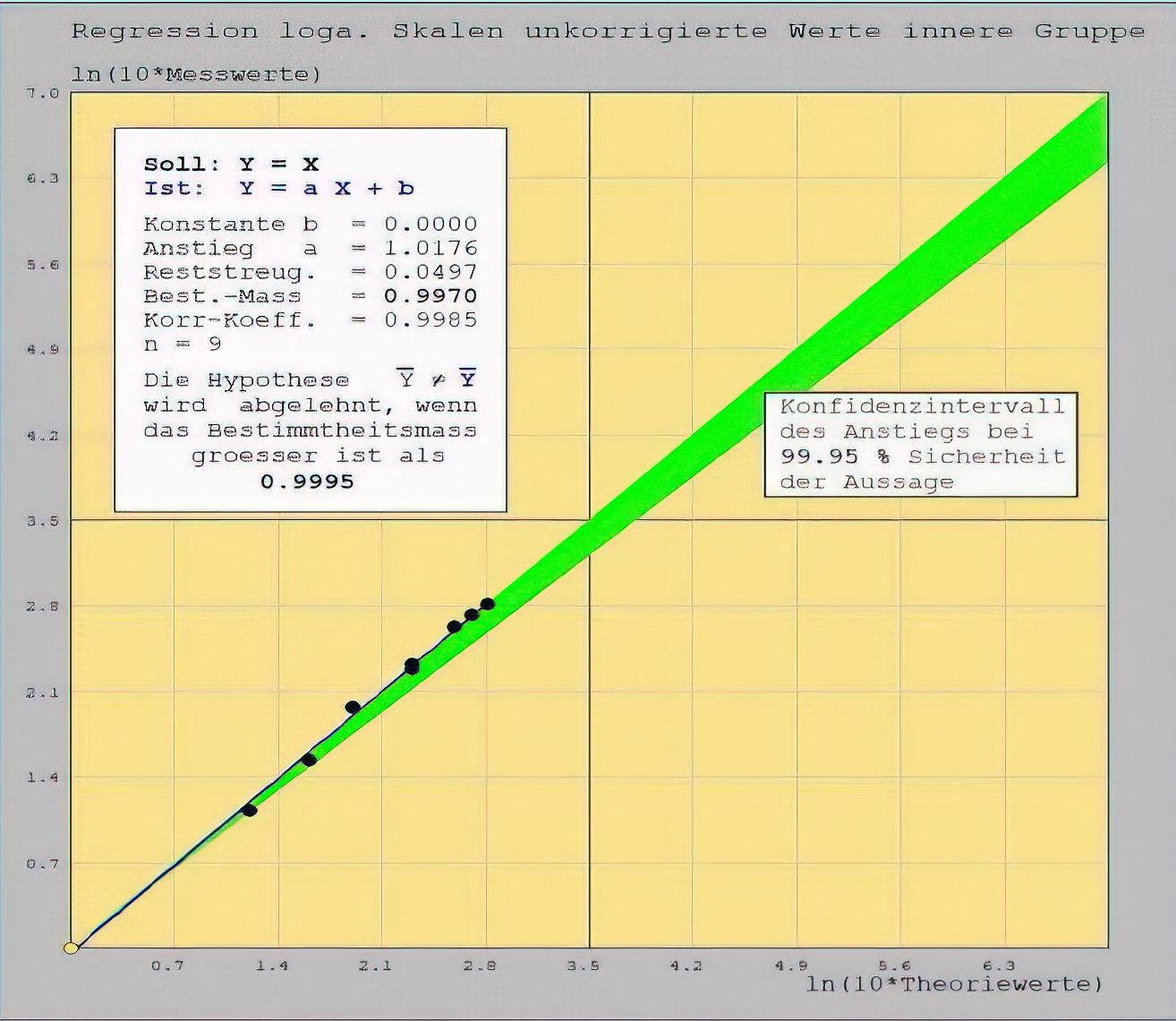
Die Korrektur der Daten bezieht sich in erster Linie auf die kleineren Werte, deshalb wird die Unterordnung hier auch nur mit diesen durchgeführt. Unkorrigiert ergibt sich: die These "Theorie = Praxis" wird abgelehnt.

Korrigiert man die Daten der betroffenen Gruppe, so wird die These „Praxis = Theorie“ nicht abgelehnt. Die Datenkorrektur macht also einen deutlichen Unterschied aus.
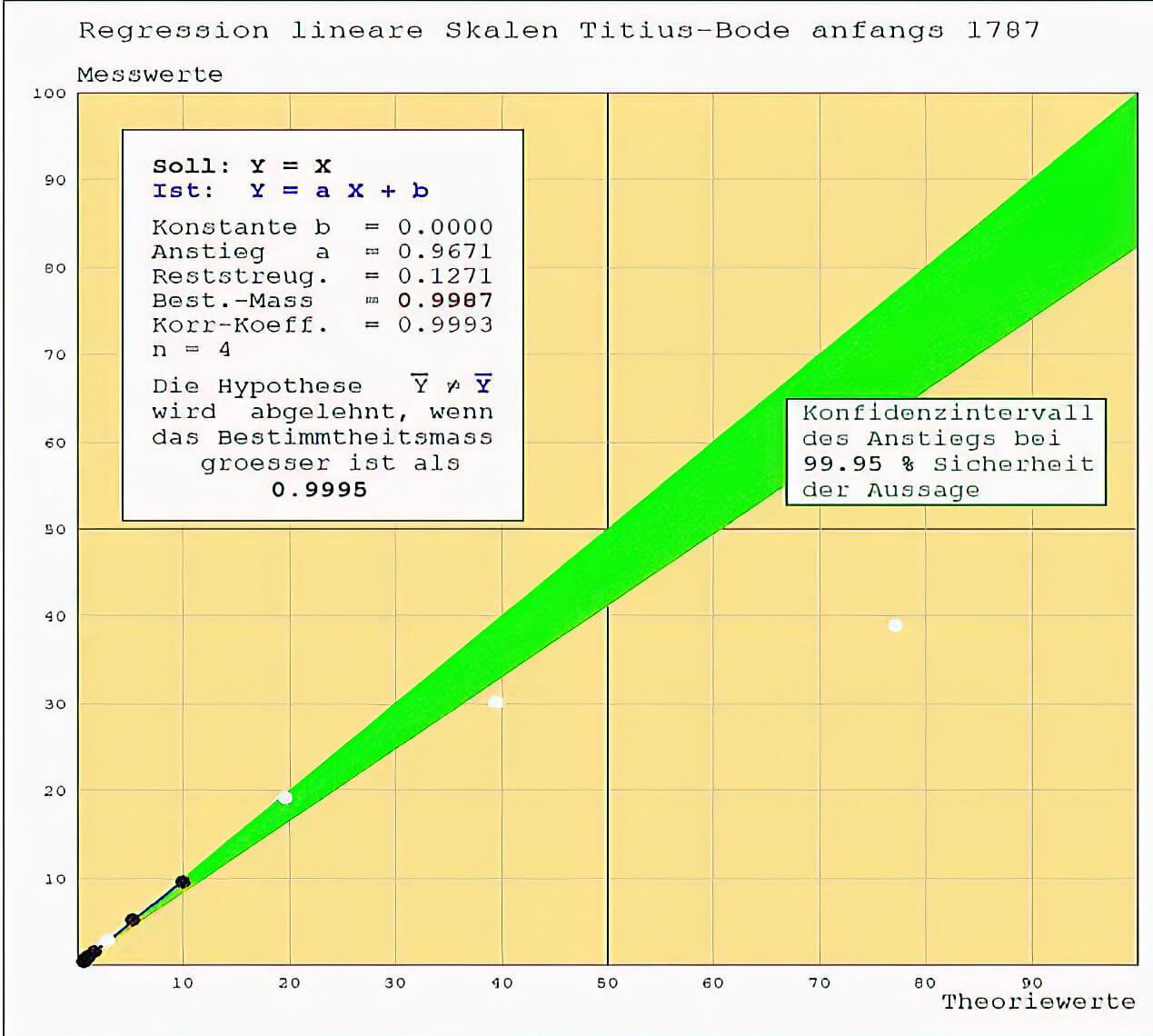
Als Vergleich, wie das Verfahren arbeitet, werden vier Phasen zur Titius-Bode-Reihe heran gezogen.
1. der Zustand 1787 nach Einführung der Astronomischen Einheit durch Johann Friedrich Wurm. Aufgrund des geringen relevanten Datenumfangs (durch zwei Konstanten werden die Freiheitsgrade reduziert) müsste die These, diese Reihe beschriebe die Datenwirklichkeit, abgelehnt werden. Es zeigt sich deutlich, dass das Anstiegskriterium versagt.
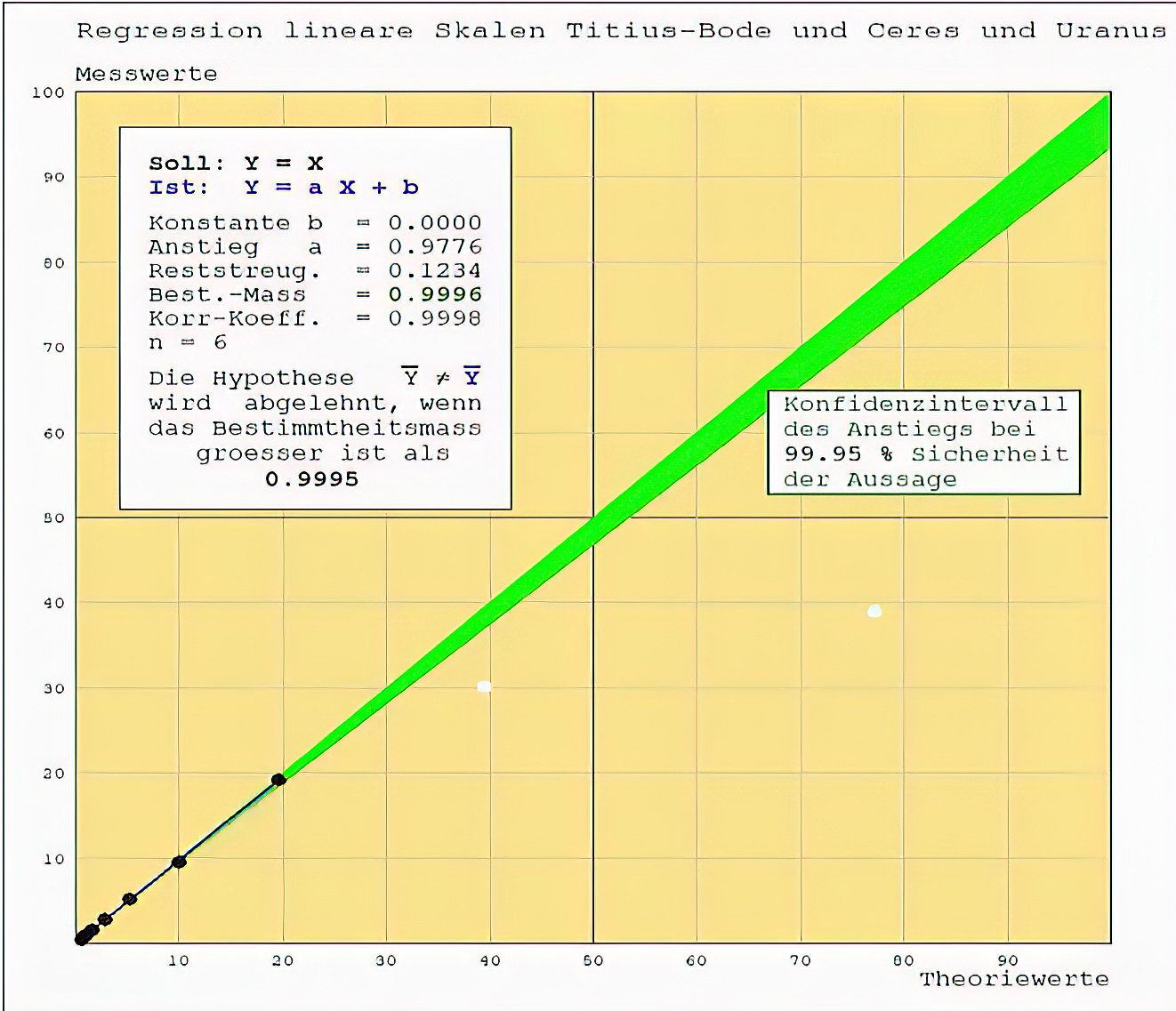
Nach Entdeckung von Uranus 1781 durch Wilhelm Herschel und Ceres 1801 durch Giuseppe Piazzi änderte sich die Situation. Hier hätte statistisch die Aussage, dass die Titius-Bode-Reihe die Wirklichkeit richtig beschreibt, nicht abgelehnt werden können und die Suche nach einem physikalischen Hintergrund war berechtigt.

1846 änderte sich die Situation drastisch durch die Entdeckung des Planeten Neptun durch Urbain Le Veısier. Die Hypothese, die Titius-Bodesche Reihe wäre zur Beschreibung der Planetenabstände geeignet, musste nun abgelehnt werden.
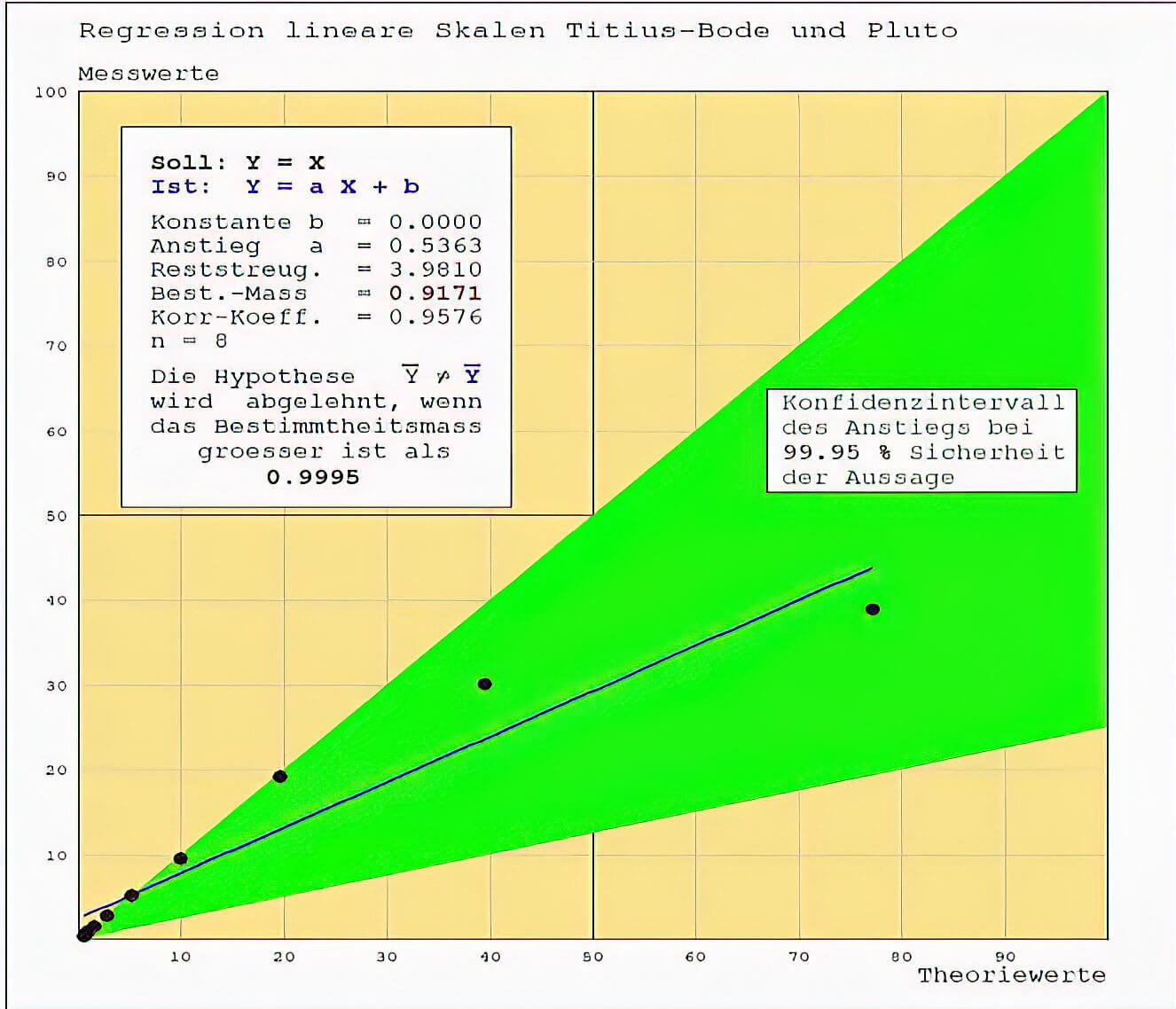
Auch mit der Entdeckung von Pluto 1930 verbesserte sich die Lage nicht, obwohl der mittlere Abstand nun dem des Planeten Neptun glich. Deutlich zeigt sich, dass die Titius-Bodesche Reihe eher einer parabolischen als einer linearen folgt und die Ablehnung der These, diese Reihe beschriebe die Wirklichkeit immer stärker wurde.
Das war vielleicht auch der Grund, warum sich seit dem kaum noch jemand darum bemühte, nach einem physikalischen Grund für die Bahnlagen der Planeten zu suchen.
Fazit: Um einen Zusammenhang sicher annehmen zu können, sollte die Aussagesicherheit >99,95% sein.
Die ersten beiden Regressionen zeigen einen Unterschied zwischen der Betrachtung in linearem oder logarithmischem Maßstab. Für eine gute Aussage sollte bei Regressionen eine möglichst gleichmäßige Verteilung der Werte vorliegen, noch besser eine Normalverteilung. Ist das wie bei unseren Daten nicht gegeben, denn im linearen Maßstab sind die niedrigen Werte unabhängig von ihrer eigenen Fehlerrate praktisch nicht wirksam und sie müssten als ein Wert betrachtet werden, was Minderung des Stichprobenumfanges und Vergrößerung des Konfidenzintervalls bedeutet.
In logarithmischen Koordinaten liegt eine gleichmäßigere Verteilung annähernd vor und deshalb sind deren Aussagen vertrauenswürdiger. Da man auf sichere Übereinstimmung zwischen gemessenen und theoretischen Daten überprüfen möchte, also eigentlich die Hypothese "Y-gemessen" gleich "Y-theorie" abzulehnen versucht, könnte man den Anstieg und sein Konfidenzintervall heranziehen. Die Bilder zeigen aber, dass durch die Spreizung der Werte damit keine brauchbaren Aussagen erzielt werden können. Geeignet erscheint stattdessen das Bestimmtheitsmaß. Es drückt das Verhältnis der Reststreuung zur gemischten Streuung der Werte selbst aus und sein Konfidenzintervall wird über die Student- oder t-Verteilung mit Tabellen bestimmt. Die höchste Sicherheitsstufe, die man dort für einseitige Fragestellung finden kann, beträgt 0.005. Ist also der ermittelte Testwert für das in der Regression erzielte Bestimmtheitsmaß größer als der Tabellenwert zum Stichprobenumfang, dann wird die These "Theorie gleich Messung" abgelehnt. Vereinfacht kann man einfach schauen, ob das erzielte Bestimmtheitsmaß größer als 99.95 % ist, um davon auszugehen, zwischen Theorie und Praxis besteht kein Widerspruch.
Die Abbildungen zeigen auch die signifikante Wirkung der Störungskorrektur. Zum Vergleich wird die Wirksamkeit dieses Verfahrens anhand der Titius-Bodeschen Reihe in vier zeitlichen Stufen deutlich gemacht und zeigt, dass man 1787 noch nicht von einem gesicherten Zusammenhang zur Realität hätte ausgehen können, erst mit der Entdeckung von Uranus und Ceres wäre das eingetreten. Und es zeigt auch, dass trotz statistisch hoher Sicherheit dies falsch war, denn ab der Entdeckung von Neptun und später gar Pluto war es vorbei mit der sicheren Aussage. Können wir auch mit unseren Zahlen und ihrer theoretischen Interpretation falsch liegen? Was sind das eigentlich für Zahlen und welche Theorie liefert die angegebene Lösung? Vielleicht ahnt es schon jemand, im nächsten Abschnitt dazu mehr.
Die Zahlen sind natürlich nicht zufällig gewählt. Es sind echte Messergebnisse, denn es handelt sich um Apsidenwerte und auch mittlere Abstandswerte der Planeten unseres Sonnensystems (gemessen in AE = mittlerer Abstand der Erde von der Sonne). Bleibt also die Frage: welche Theorie führt zu der angegebenen Lösung? Auch die ist bereits benannt worden, es ist die Makroquantentheorie und man erhält die Lösung über einige Rechenschritte direkt aus der Hauptgleichung, die bis auf eine physikalische Größe mit der Schrödingergleichung


Die (eigentlich interessierende) Wahrscheinlichkeitsdichte 

Wie kommt die bereits oben angegebene Lösungsformel zustande?


Die COS²-Funktion hat Maxima, wo das Argument ganzzahligen Werten von "π" entspricht, die SIN²-Funktion bei halbzahligen. Somit existieren zwei Lösungsarten

Nun erklärt sich auch der in der 2. Tabelle rot gekennzeichnete Wert nicht als Untergruppe mit m = 2 zur Gruppe m = 1, l = 2 sondern als Sinuspendant zur Gruppe m = 1, l = 2 mit n = 0. Folglich sollte es auch zur Cosinusgruppe für n = 0 einen Wert geben, das ist in der Tat das Zentralgestirn.
In den folgenden Darstellungen sind die Umlaufbahnen (korrigiert und unkorrigiert) der Planeten einem Wellenbild überlagert, das die Wahrscheinlichkeitsdichte der entsprechenden SINUS²- oder COSINUS²-Funktion wiedergibt, wobei die Maxima hell und die Minima dunkel erscheinen. Die Apsidenlage ist ausgerichtet, die Periapside (Nahpunkt) liegt für alle Bahnen rechts, entsprechend die Apoapside (Fernpunkt) links. Je Bild ist nur stets eine Wellenlänge wirksam, Überlagerungen, wie sie in der Realität vorkommen, sind der besseren Erkennbarkeit halber vermieden.
Sieben Darstellungen aller Planetenbahnen und der zugeordneten Wellen mit zusätzlich angenommenen Bahnen:



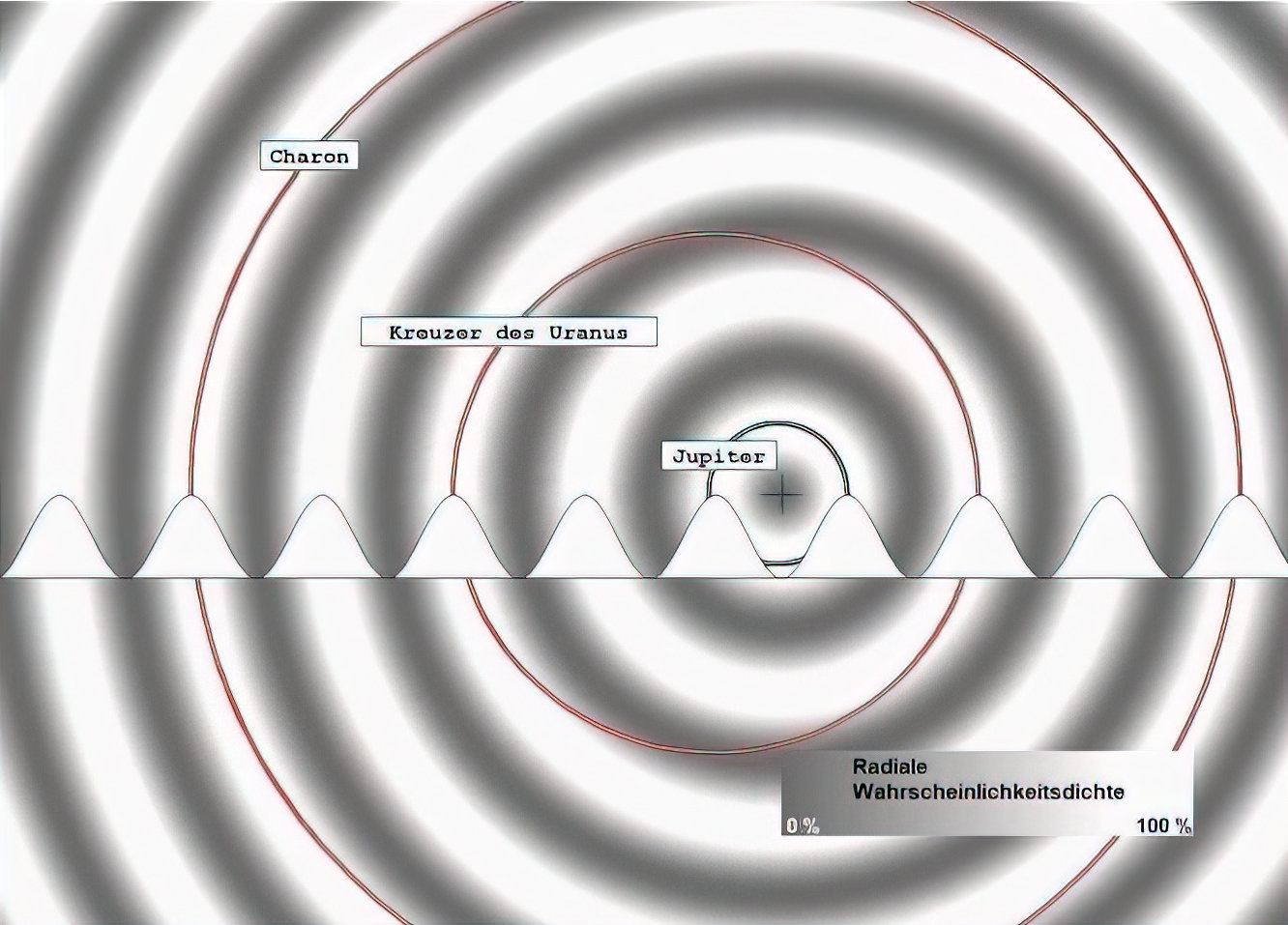
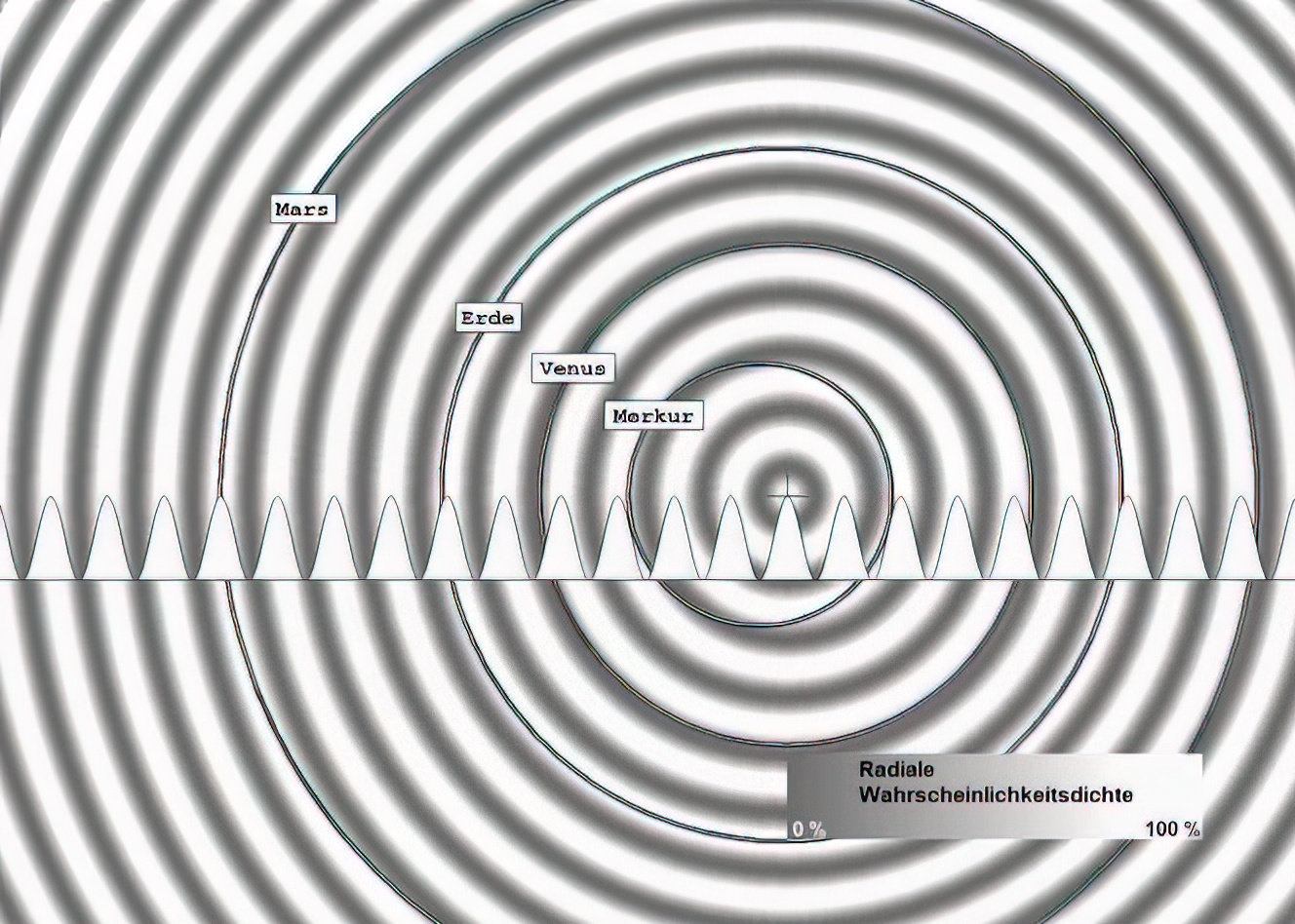
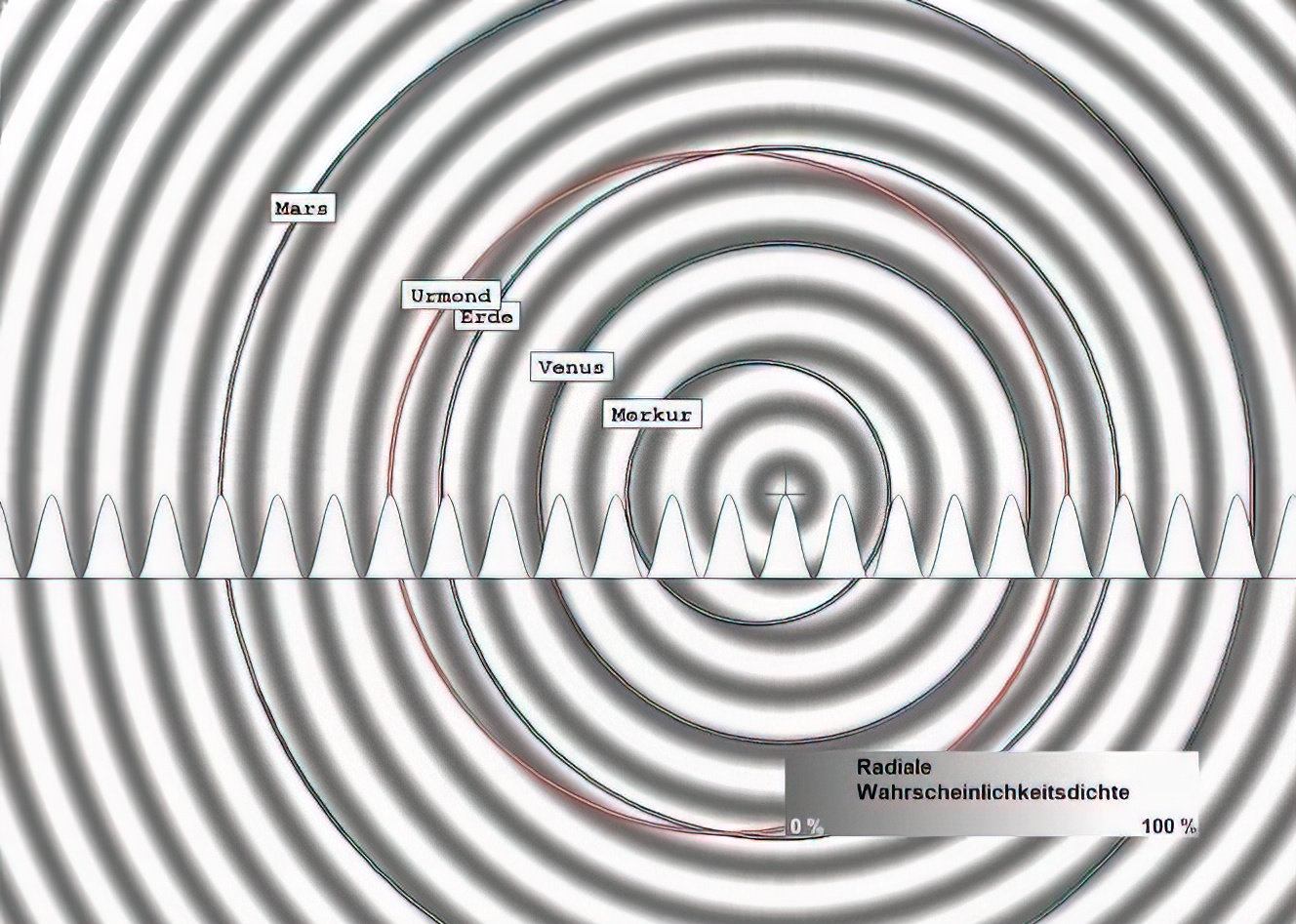
Fällt Ihnen bei diesen Darstellungen etwas auf? Wahrscheinlich nicht. Mir ist, als ich euphorisch die Zusammenhänge überprüfte und begeistert war von der kompletten Übereinstimmung, erstmal auch nichts aufgefallen. Zu überzeugend waren die Übereinstimmungen von astronomischen Daten und den Voraussagen der Theorie mit ihren Lösungsfunktionen, den harmonischen Wellen.
Halt!
Harmonische Wellen? Das sind doch Wellen, ohne dass eine Kraft wirkt.
Bewegen sich Planeten ohne Kraftzentrum? Was ist dann die Sonne mit ihrer alles zusammenhaltenden Gravitationskraft? Als mir das dämmerte, durchfuhr mich ein großer Schreck: meine Theorie funktioniert bei den Planeten und anderen Himmelskörpern nur, wenn man das Kraftzentrum negiert.
Die Suche nach der Ursache dieses Konfliktes war gar nicht so einfach. Dann aber wurde ich fündig. Während meines Studiums war ich nie damit konfrontiert worden, meine Lehrbücher der Theoretischen Physik erwähnten nichts davon. In den frühen 1970er Jahren war sie zwar bereits etabliert, aber nur etwas für Experten und Spezialisten - Einsteins Allgemeine Relativitätstheorie (ART). Dort erfuhr ich, dass diese Theorie die Gravitation als Raum- und Zeitkrümmung beschreibt und die Bewegung von Himmelskörpern auf Geodäten erfolgt, die zwischen zwei beliebigen Bahnpunkten stets die kürzeste Entfernung bilden und auf denen alle antriebslosen Bewegungen kräftefrei vor sich gehen, egal, ob sie wie bei elliptischen Bahnen von ferne betrachtet in ständiger Beschleunigung und Abbremsung scheinen. Wenn nur kräftefreie Lösungen meiner Theorie bei der Behandlung himmelsmechanischer Probleme zu richtigen Ergebnissen führen, dann heißt das, die ART muss geradezu zwingend vorausgesetzt werden und im Hamiltonoperator
Diese wichtige Aussage hat mich zur Überzeugung gebracht, dass die drei Kräfte nicht mit der Gravitation zu vereinheitlichen sind, weil Gravitation gar keine Kraft, sondern eine geometrische Eigenschaft ist, die nur durch Energie (Masse) hervorgerufen und nicht von Austauschteilchen vermittelt wird.
Die regulären Bahndarstellungen erklären sich fast von selbst. Die Wirkung der Korrektur, die den offensichtlich durch Störung hervor gerufen Einfluss rückgängig macht und zu signifikant besseren Werten führt, ist deutlich sichtbar.
Das Diagramm zur Saturnserie zeigt zwei Dinge. Bei bedeutenden Welleneinflüssen sind zum einen alle Maxima besetzt und es gibt zum anderen Planeten, die zwischen verschiedenen Maxima pendeln (Pluto). Damit ist es berechtigt, bei der Welle der inneren Planeten nach der Ursache der unbesetzten Maxima 1, 5 und 7 zu fragen. Ist das vakante 1. Maximum noch einfach mit der großen Sonnennähe erklärbar, sieht es beim 5. und 7. anders aus. Dass jeweils je ein Planet auf diesen Maxima war, kann ausgeschlossen werden, da es keinen physikalischen Mechanismus gibt, der Planeten spurlos verschwinden lässt. Dass zufällig gerade dort keine Materie zur Bildung eines Planeten gewesen sein soll, ist auch nicht wahrscheinlich. Bleibt also nur die Möglichkeit anzunehmen, dass ursprünglich ein Planet zwischen 5 und 7 pendelte. Für sein Verschwinden spricht einiges, denn er besaß zwei Kreuzungspunkte mit der Erdbahn. Die gleichen mittleren Entfernungen der Erde und dieses Planeten zur Sonne, führen zu einer Begegnung mit gleichem Geschwindigkeitsbetrag (nur die Bewegungsrichtungen differieren etwas). Eine solche Begegnung kann zu einem Einfang oder einer Kollision führen. In beiden Fällen hinterbleiben Spuren. Für einen Einfang spricht, wenn an den "Lagrange-Punkten" 4 und 5 im System Erde-Mond keinerlei Restmaterie von einer Kollision zu finden ist. Ein Planeteneinfang (auch Kollision) erzeugt eine Störung auf alle benachbarten Planeten, deren Einfluss sich nachweisen lässt, weil (noch nicht erklärbar) eigenartigerweise die Korrekturen in ganzzahligen Portionen der Wellenlänge von 1/60 AE liegen, was gleichzeitig sehr genau dem Abstand der heutigen Erdapsiden von der mittleren Erdbahn-Entfernung entspricht. Es bleibt die Schlussfolgerung, der ursprünglich zwischen den Maxima 5 und 7 der inneren Welle pendelnde Planet hat nach einem Crash den Mond gebildet, wahrscheinlicher aber ist er durch Einfang zum heutigen Mond geworden.
Nach analogem Prinzip wurde bei der Welle verfahren, die zum Jupiter gehört. Auf dieser SIN²-Welle existiert nur noch ein belegtes Maximum (Jupiter). Die nicht (mehr) besetzten Maxima 2 - 5 gehören zu Bahnen mit Kreuzungspunkten zur COS²-Welle der Saturnserie. Und tatsächlich lassen sich an den beteiligten Planeten der Saturnserie Besonderheiten finden.

Uranus hat als einziger Planet eine stark von allen anderen Planeten abweichende Achsneigung, die von der Astronomie ohnehin als Folge eines Zusammenstoßes gedeutet wird.
Plutos Mond Charon fällt größenmäßig völlig aus dem Rahmen und passt nicht zum Wellenpaar COS² und SIN² der anderen Plutomonde. Dieses Wellenpaar (cos² und sin²), das auf das Baryzentrum ausgerichtet ist, beschreibt die vier kleinen Monde recht gut, nicht jedoch Charons Umlauf. Dessen große Masse im Vergleich zu Pluto (ca. 12 %) führt dazu, dass Pluto selbst das Baryzentrum umkreist.
Die entsprechenden Werte der Wahrscheinlichkeitsdichte sind an den Bahnapsiden angegeben und machen diesen Zusammenhang deutlich.
Bisher sind immer nur Wellen einer Wellenlänge und eine dazugehörende Störung betrachtet worden. Von Interesse ist aber auch, ob in einem Wellenzusammenhang der Einfluss einer anderen Welle nachgewiesen werden kann. Deshalb wird untersucht, ob bei den Planeten der Saturn- und Jupiterserie mit ihrer wesentlich größeren Wellenlänge eine Wirkung der kleineren Wellenlänge der Serie der inneren Planeten nachzuweisen ist.
Dazu werden Apsidendifferenzen und Apsidenabweichungen vom theoretischen Wert betrachtet.
Anmerkung: Bei großen Werten führt das Zurückführen auf n/6 bzw. m/60 AE (n und m sind ganze Zahlen) zu immer kleineren Abweichungen, wenn man mit dem Wert selbst vergleicht. Hier muss die Abweichung zum Wert 1/6 AE für den Welleneinfluss betrachtet werden und für den Störeinfluss zu 1/60 AE.
Die genutzten Werte stammen von der "NASA" (Stand 27.06.21 und sind auf AE umgerechnet).

Jupiter hat die Apsidenwerte 4.95008 AE und 5.45875 AE.
Deren Differenz (Apoapsidenwert - Periapsidenwert) von 0.50867 kann dargestellt werden als 3/6 = 0.5 mit dem Rest 0.00867 (Abw. zu 1/6 ~ 5.2 %) und spricht für den Einfluss der Welle mit 1/6 AE Wellenlänge.
Die Periapside weicht vom theoretischen Wert π2/2 = 4.93480 um 0.01528 AE (9.1 % zu 1/6 AE) ab, kann aber durch π2/2 + 1/60 = 4.95147 AE mit einer Abweichung von 0.0013 AE (~ 8.3 % in Bezug auf 1/60 AE) auch den Störeinfluss schwach zeigen.
Die Apoapside folgt π2/2 + 3/6 = 5.43480 AE mit der Abweichung von 0.02395 AE, was einem Wert von 14 % bezogen auf 1/6 AE entspricht.
Fazit: Die Apsidendifferenz zeigt nur den Einfluss der Welle 1/6 AE (94 % Wahrscheinlichkeit). Die Periapside liegt mit 91 % Wahrscheinlichkeit auf der SIN²-Welle π2/2. Ein Störeinfluss von 1/60 AE zeigt sich mit ~ 92 % Sicherheit. Die Apoapside liegt mit 86 % Wahrscheinlichkeit ebenfalls dort, wenn man die Apsidendifferenz 3/6 AE berücksichtigt. Ein Störeinfluss ist, wenn überhaupt nur schwach nachweisbar.
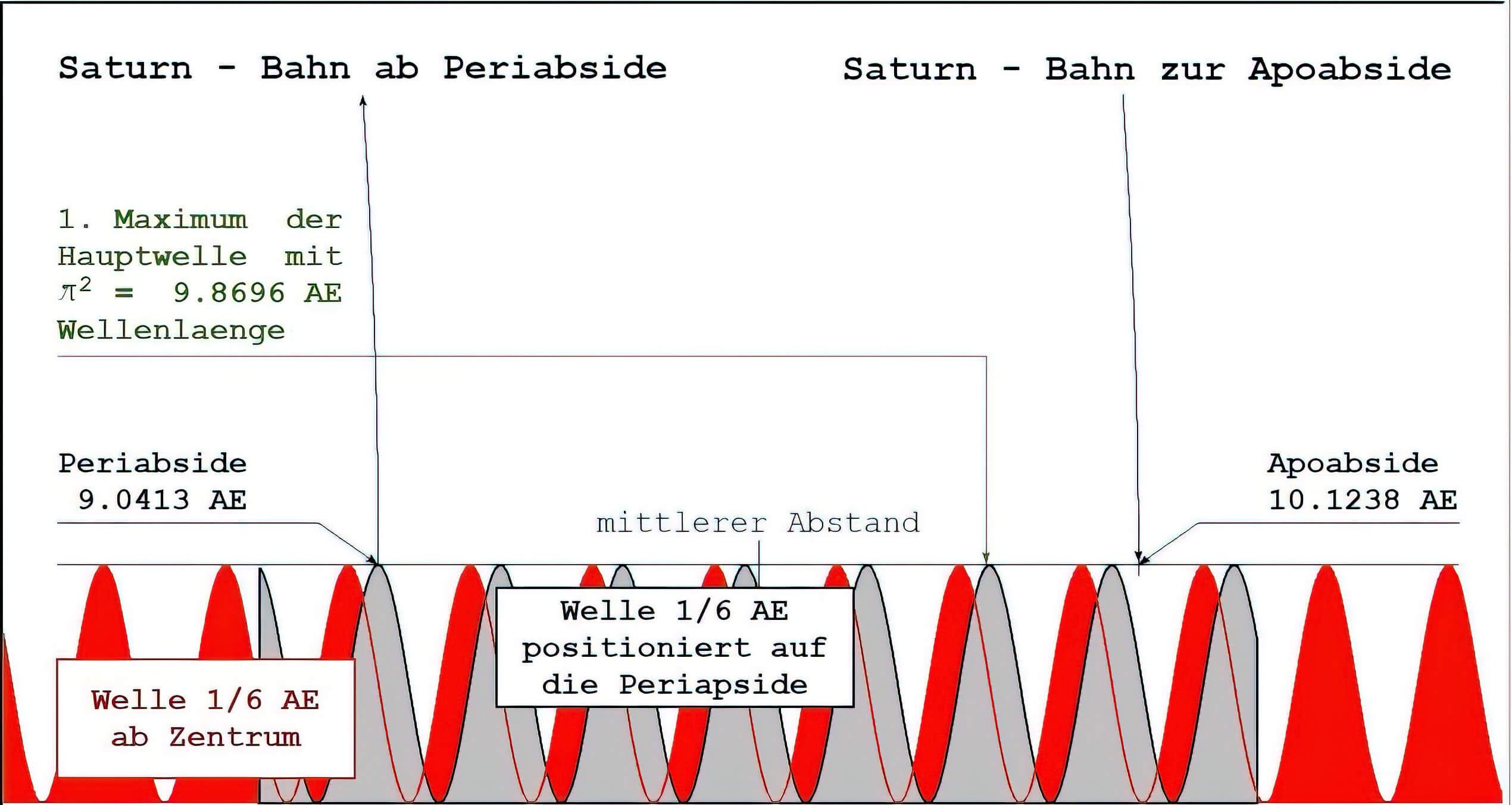
Saturn hat die Werte 9.04127 und 10.12383.
Die Differenz beträgt 1.08326. Der Wert 6.5/6 = 1.08333 AE weicht davon um 0.00077 AE (~ 0.5 % auf 1/6) ab, was bedeutet, hier liegt eine Apside auf der SIN²- und die andere auf der COS²-Welle und der Einfluss der inneren Welle (1/6 AE) ist deutlich.
Die Periapside weicht vom theoretischen Wert 9.86960 AE um 0.82833 AE ab und ist mit π2 - 5/6 = 9.03627 und mit einer Abweichung von 0.00500 AE (2.9 % von 1/6 AE) gut zum Nachweis des Welleneinflusses geeignet. Ein Störeinfluß ist nicht nachweisbar
Die Apoapside lässt sich mit π2 +1.5/6 = 10.1196 ebenfalls recht gut beschreiben (Abweichung 0.00423 AE ~ 2.5 % bezogen auf 1/6). Auch hier ist kein Störeinfluss erkennbar.
Fazit: Die Apsidendifferenz zeigt sehr deutlich den Einfluss der Welle 1/6 AE (97 %) und zugleich, dass sowohl der Sinus- als auch der Cosinusteil wirken. Die Apsiden selbst liegen gut auf der Welle 1/6 AE, die Periapside auf dem Cosinus-Anteil (97 %) und die Apoapside auf dem Sinusteil (97 %). Ein Störeinfluss der Größenordnung 1/60 AE kann mit gleicher Sicherheit ausgeschlossen werden.
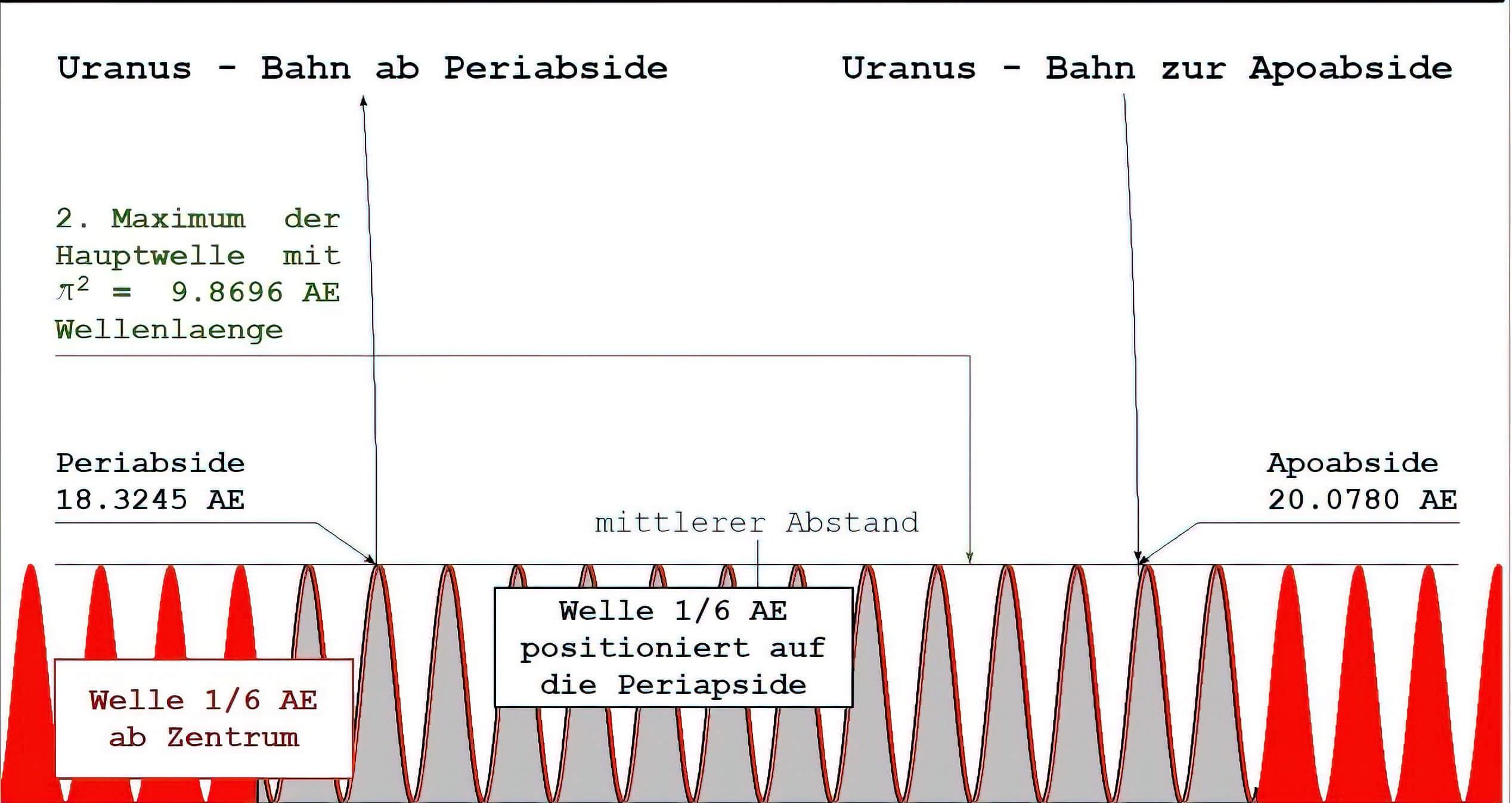
Uranus hat Apsiden bei 18.32447 und 20.07799 AE.
Das ergibt eine Differenz von 1.75352 AE. Diese weicht von 10.5/6 um 0.00352 AE (2.1 % zu 1/6) ab. Auch hier wirkt sowohl die COS²- als auch die SIN²Welle.
Die Periapside weicht vom theoretischen Wert 2π2 = 19.73921 AE um 1.41474 AE ab, was sich mit dem Welleneinfluß von 8.5/6 = 1.41667 AE erklärt und einen Rest von 0.00193 AE läßt. Der Welleneinfluß 1/6 AE zeigt sich mit 98.8 % Wahrscheinlichkeit. Die Apoapside weicht von 120.5/6 = 20.0833 AE um 0.00534 AE, also nur um ~ 3 % ab.
Die Abweichung vom theoretischen Wert 19.73921 beträgt 0.33878 AE, was 2/6 AE mit einer Differenz von 0.005 AE entspricht, also zu 97 % durch die Welle 1/6 AE beeinflusst ist.
Fazit: In der Apsidendifferenz ist der Welleneinfluß 1/6 AE (Sinus- und Cosinusanteil) gut zu erkennen. Sowohl die Periapside als auch die Apoapside zeigen einen gut gesicherten Zusammenhang zur Welle 1/6 AE. Ein Störeinfluss kann auch hier mit gleicher Sicherheit ausgeschlossen werden. In der Grafik sieht es eher nach einer Apsidendifferenz von 11/6 AE aus, die obigen Zahlen sind aber genauer.
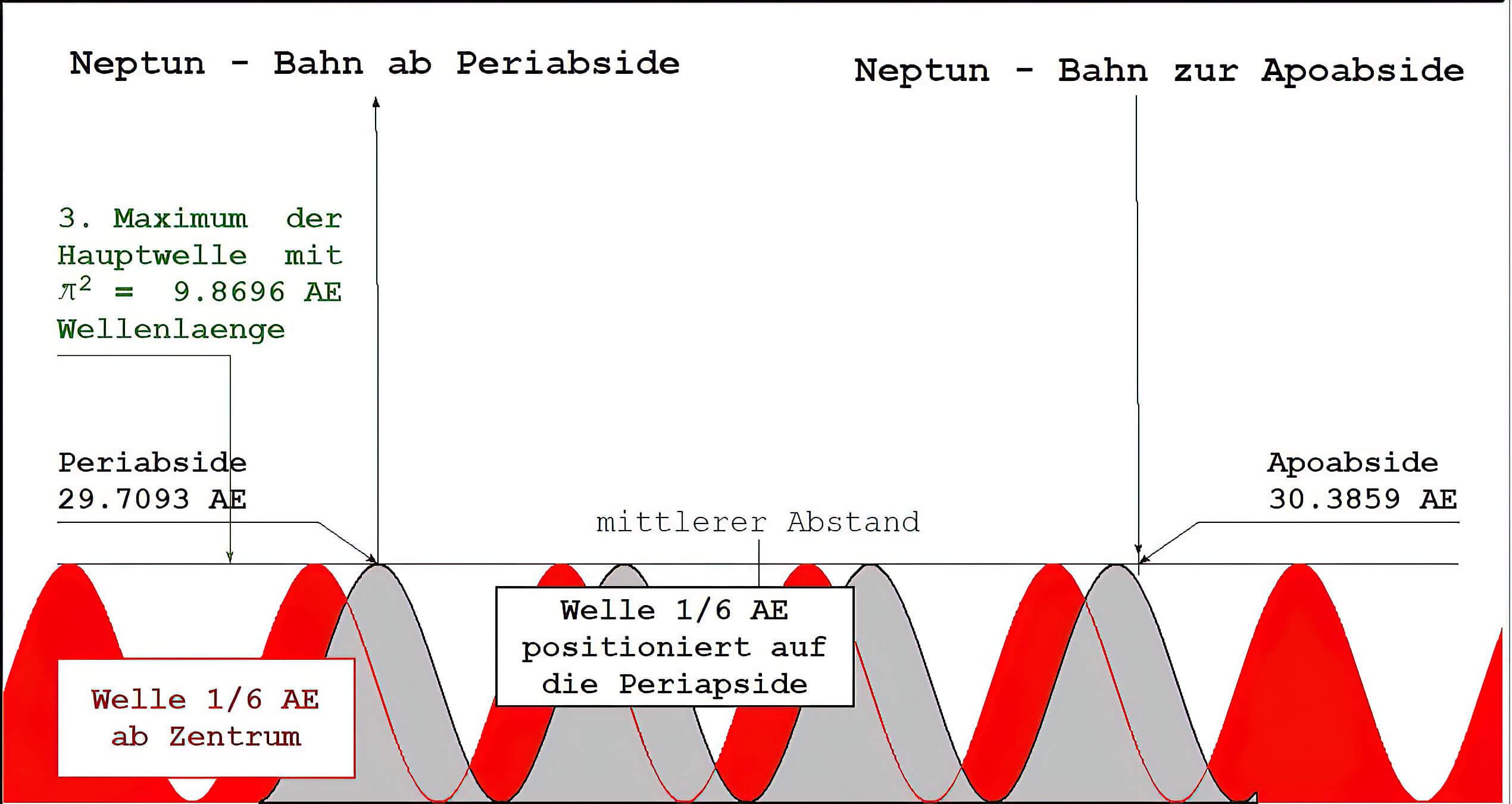
Neptuns Apsidenwerte liegen bei 29.70930 und 30.38593 AE.
Ihre Differenz ist 0.61663 AE => 4/6 = 0.66667 weicht um 0.05004 AE davon ab, 30 % auf 1/6. Aber 4/6 - 3/60 = 0.61667 weicht nur um 0.000037 AE (0.22 % bezogen auf 1/60) ab.
Die Periapside sollte theoretisch bei 29.60881 AE liegen. Sie weicht davon um 0.0933 AE ab was mit 0.5/6 AE = 0.0833 zu 6 % Abweichung bezogen auf 1/6 AE führt.
Die Apoapside weicht vom theoretischen Wert 29.385 um 0.808 AE ab und selbst mit der Annahme des Welleneinflusses 1/6 AE mit 5/6 = 0.8333, also dem Rest von 0.025 AE, wäre die Wahrscheinlichkeit dafür, dass der Welleneinfluß wirkt, nur ~ 84 %.
Fazit: Die Apsidendifferenz deutet zunächst nur schwach auf einen Einfluss der Welle 1/6 AE hin, aber nimmt man den Störfaktor 1/60 AE hinzu, dann ist sowohl der Einfluss der Welle 1/6 AE als auch der Störfaktor 1/60 mit 96 % sicher zu erkennen.
Die Abweichungen der Apsiden selbst lassen sich weder auf die Welle 1/6 AE noch auf den Störfaktor zurückführen.
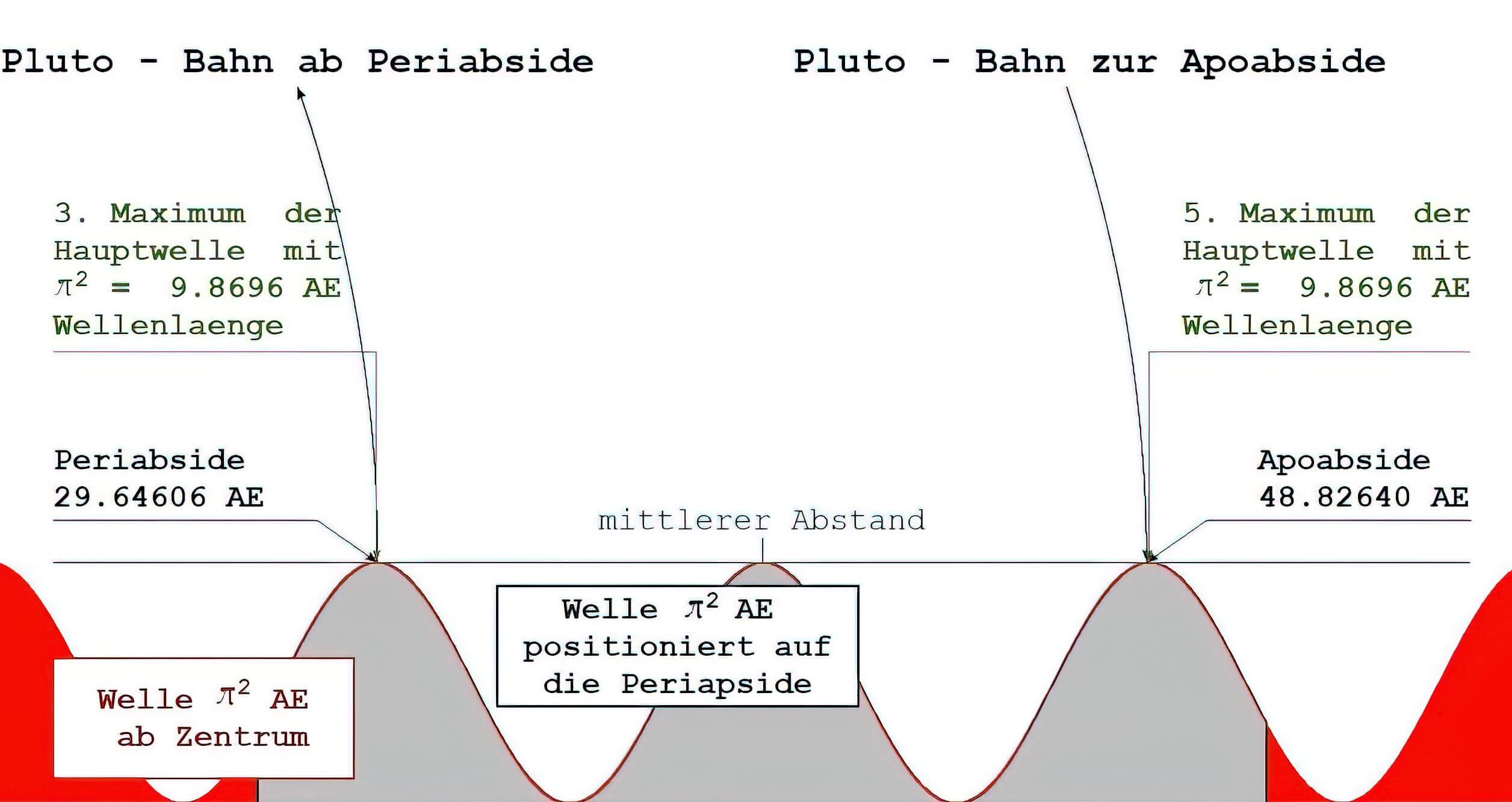
Pluto belegt die Maxima 3 und 5 der COS²-Welle π2 AE und besitzt astronomisch Apsiden bei 29.658 und 49.304 AE. Es scheint nicht viel Sinn zu machen, deren Differenz auf 1/6 AE hin zu prüfen. Dennoch ergibt die Differenz den Wert 19.646 AE, der sich erstaunlich gut durch 118/6 = 19.6666 darstellen lässt und davon nur um 0.02 AE (~ 12 % zu 1/6) abweicht.
Die Periabside liegt theoretisch auf dem Wert 3π2 = 29.6088 AE und weicht vom astronomischen Wert um 0.049 AE (~30 % zu 1/6) ab. Nimmt man jedoch die Störung 3/60 AE hinzu, dann ergibt das 3π2 + 3/60 = 29.6588 AE und die Differenz beträgt 0.0008 AE (~ 5 % zu 1/60). Die Abweichung wird also mit 95 % Wahrscheinlichkeit durch die Störung verursacht.
Die Apoapside sollte auf dem 5. Maximum liegen und den Wert 49.348 AE haben. Sie weicht um 0.044 AE ab. Diese Abweichung ist weder mit der Welle 1/6 AE noch mit der Störung 1/60 AE zu erklären.
Fazit: An der Apsidendifferenz lässt sich nur mit geringer Wahrscheinlichkeit ein evtl. Einfluss der Welle 1/6 AE zeigen (88 %).
Die Periapside zeigt den Einfluss der Störung (95 %), aber nicht den der Welle 1/6 AE. Aus der Apoapsidenlage sind keine Hinweise zu ziehen.
Gesamtergebnis: Der Einfluss der Welle 1/6 AE auf Objekte der Welle π2 AE ist in den Apsidendifferenzen mit leicht abnehmender Sicherheit (99 % -> 88 %) bei allen Planeten von Jupiter bis Pluto gut nachweisbar. Ebenso an den Apsiden von Jupiter und Saturn, sowie der Apoapside des Uranus.
Der Störeinfluss 1/60 AE wirkt nur nachweisbar auf die Apsidendifferenz des Neptun und die Periapside des Pluto. Andererseits kann eine Wirkung der Störung auf Jupiter und Saturn mit mehr als 90 % Sicherheit ausgeschlossen werden. Das ist verständlich und vereinbar mit der obigen Annahme, die Störung hänge mit dem System Erde-Mond zusammen, da große Planeten wie Jupiter und Saturn durch Störungen wohl kaum beeindruckt werden, durch andere Wellen während ihrer Entstehungsphase schon eher. Kleinere Objekte weisen außer dem Welleneinfluss durchaus auf den Störeinfluss hin.
Bei den inneren Planeten, die der Welle 1/6 AE folgen, wird nur auf den Störeinfluß 1/60 AE geachtet, die Positionierung wird im Gegensatz zu den äußeren Planeten nicht auf die Periapside, sondern auf die Apoapside gemacht.
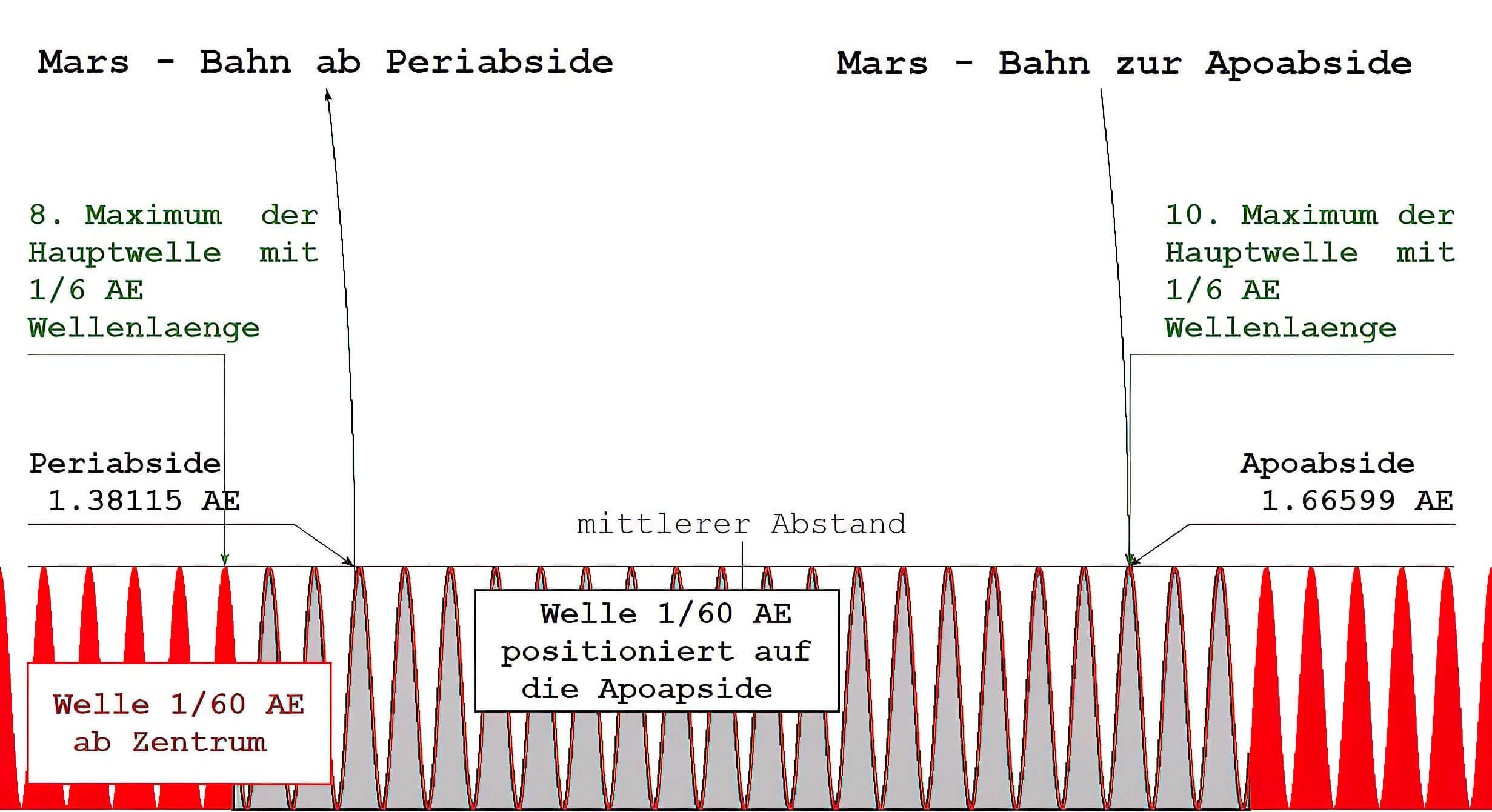
Mars besitzt Apsiden bei 1.38114 und 1.66599 AE. Ihre Differenz beträgt 17.09 Wellenlängen 1/60 AE, weicht demnach um ca. 0.5 % vom exakten Wert 17 ab. Die Apoapside ist gegenüber der Welle 1/6 AE um -0.000676 AE (~ 0.4% Abw. zu 10/6 AE) verschoben, die Perabside um 0.04781 AE (~ 29 %). Von einem Störeinfluß (17/60 AE) kann ausgegangen werden.
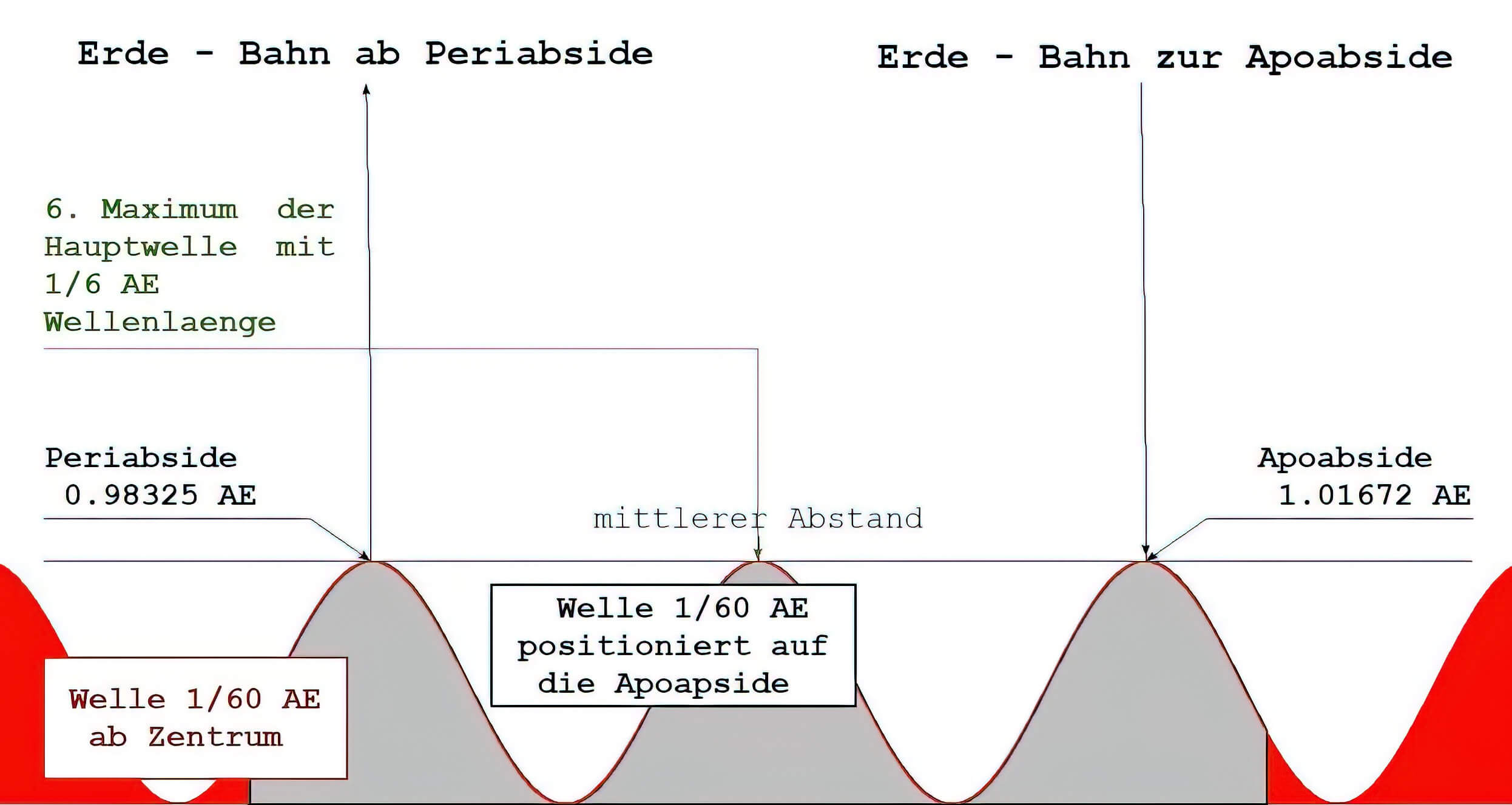
Bei der Erde liegen die Apsiden bei 0.98325 und 1.01672 AE und die Differenz beträgt 0.03347 AE, weicht also von dem Wert 2/60 AE nur um 0.8 % ab und ist (durch den Mondeinfang oder -zusammenstoß) offensichtlich Ausgang der Störung 1/60 AE.

Die Venus hat die geringste Exzentrizität, die Apsiden liegen also dicht beeinander, 0.718433 und 0.728212 AE von der Sonne entfernt. Die Differenz von 0.00978 AE zeigt keinen Zusammenhang zur Störung, auch an den Apsiden ist nichts zu erkennen.
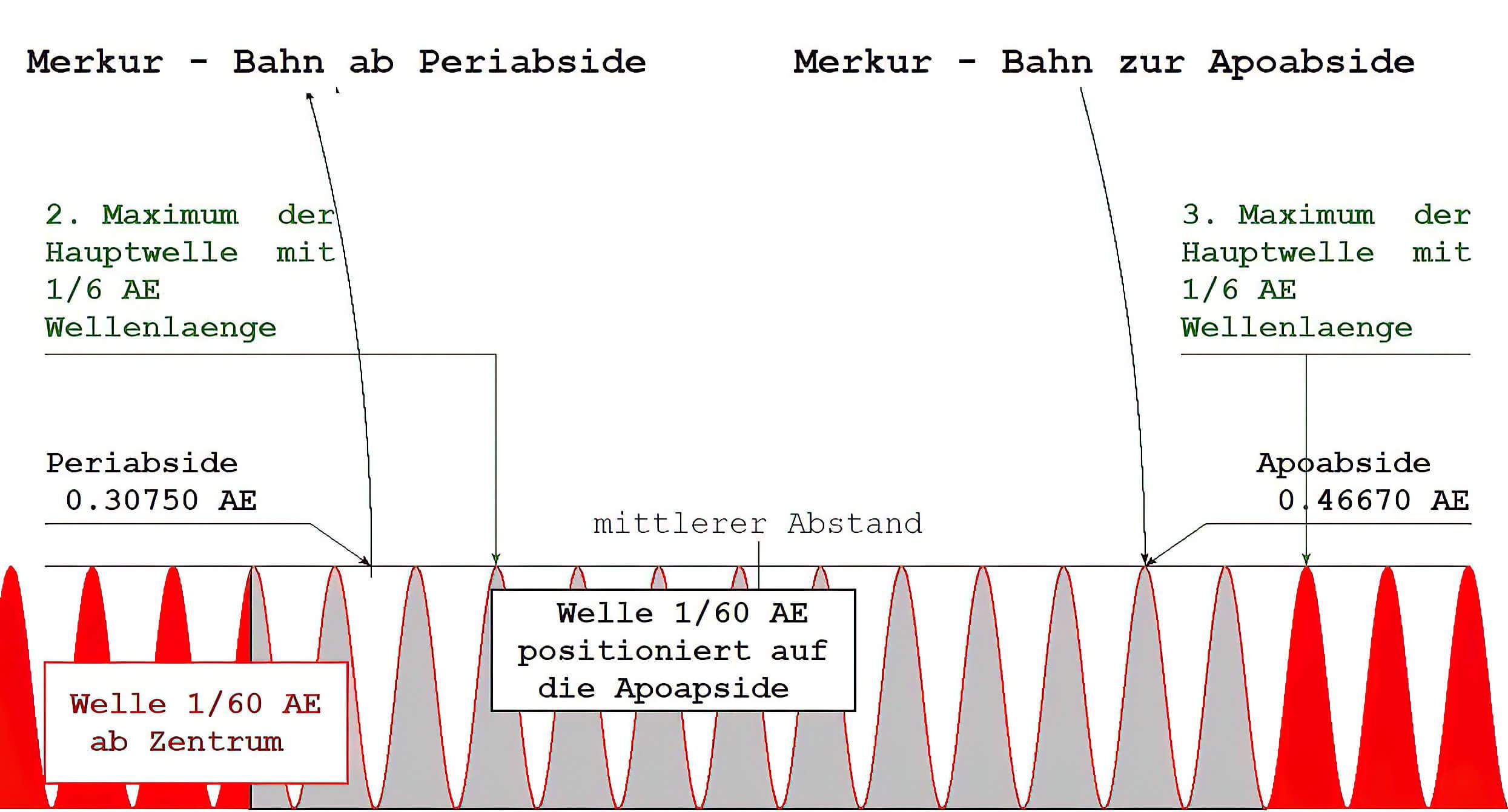
Beim Merkur hingegen ist der Einfluß 1/60 AE besonders an der Apoapside deutlich. Sie liegt bei 0.466698 AE und weicht vom Wert 3/6 AE (3. Maximum der inneren Hauptwelle mit 1/6 AE Wellenlänge) um 0.033302 AE ab, was sehr genau dem Wert von 2/60 AE entspricht (Abw. nur 0.19 %). Die Periapside mit einem Wert von 0.307504 AE weicht vom 2. Maximum = 2/6 AE allerdings um 0.025829 AE ab, hat aber vom Wert 1.5/60 eine Abweichung von ca. 5 %. Beim Merkur ist der Einfluss 1/60 AE sichtbar.
Gesamtergebnis: Sehr deutlich ist der Einfluss einer als Störung angenommenen Wellenlänge von 1/60 AE bei den inneren Planeten bis auf Venus zu erkennen, mit der höchsten Präzision an der Merkurapoapside und bei den Erdapsiden.
Bisher sollte gezeigt werden, dass unser Sonnensystem bis auf die Keplerschen Gesetze nicht auf historischen Zufälligkeiten beruht, sondern einem klaren physikalischen Prinzip in seinem Aufbau folgt. Die Theorie, die dieser Nachweis liefert, ist zwar neu und weitgehend unbekannt, erfüllt aber alle Kriterien wie anerkannte Theorien auch und der Verfasser ist sicher, sie wird sich durchsetzen. Möglich ist, da sie eine Verallgemeinerung der Quantentheorie darstellt, dass sie in eine entsprechende Matrixform statt der Wellendarstellung umgewandelt wird, so wie die Schrödingersche Wellenmechanik der Heisenbergschen Matrixmechanik vergleichbar ist. Ich selbst halte die Wellendarstellung für anschaulicher.
Die Aussagen der hier vorgestellten Makroquantenphysik, die allgemein für alle existierenden Systeme gelten, zeigen: es ist zweckmäßig, von zwei Zuständen in der Struktur des Sonnensystems auszugehen, einem Urzustand während der Ausbildungsphase und einem Folgezustand, nachdem die vorprogrammierten Zusammenstöße oder Einfänge stattgefunden haben und zu Störungen der ursprünglichen Bahnen geführt haben.
Als diesen Urzustand bezeichne ich den Entwicklungsstand im jungen Sonnensystem, als sich die Planetenstruktur herausgebildet hatte, aber noch keine Störungen die Bahnen veränderten. Gemeinsam alle Planeten zu beschreiben und darzustellen, ist ihrer sehr großen Entfernungsunterschiede wegen nicht zweckmäßig. Deshalb werden die inneren Planeten getrennt von den äußeren betrachtet und hier in leicht veränderter Weise die schon weiter oben gezeigten Darstellungen genutzt.
Diese Auftrennung ist auch von der Theorie her logisch, da zwei Grundwellen der aus den Gleichungen als Lösungen folgenden Wahrscheinlichkeitsdichten das Geschehen aller hauptsächlich betrachteten Objekte vollständig und mit großer Genauigkeit beschreiben, diese Wellen in ihren Wellenlängen sich jedoch um etwa den Faktor 60 unterscheiden (6 π2 = 59.2176). So zeigen die zwei Darstellungen den Ur-Zustand der äußeren Planeten und inneren Planeten.
Die gepunkteten Bahnen sind die mittleren Abstände.
Der Folgezustand wird erreicht, wenn es keine kreuzenden Bahnen mehr gibt. Er entspricht dem heutigen. Nun sind Störungen in den ursprünglichen Bahnen erkennbar. Abschließend kann man sagen, das Sonnensystem ist ein klar strukturiertes, im Urzustand noch fast exaktes System, das durch Wellen mit zwei verschiedenen Wellenlängen dominiert ist. Die dabei auftretenden Kreuzungsbahnen (zwei in der Exzentrizität verschiedene, aber im mittleren Abstand gleiche Bahnen) führen zu Störungen, deren Einfluss sich in Änderungen der ursprünglichen Bahnen äußert, jedoch durch "gequantelte" Wirkung nachweisen lässt.
Die bisherigen Nachweise extrasolarer Planeten reichen in der Genauigkeit ihrer Bahnparameter vielleicht noch nicht aus, um zu zeigen, dass es Ähnliches wie im Sonnensystem gibt und damit eine die Allgemeingültigkeit der hier vorgestellten und anhand des Sonnensystems diskutierten Theorie abgeleitet werden kann. Einen Hinweis darauf allerdings geben die Daten von Exoplaneten, denn man hat festgestellt, dass sie größtenteils einer ähnlichen Reihe wie der Titius-Bode-Reihe folgen. Da diese keiner physikalischen Theorie entspringt, aber durch die 2n-Folge zu analogen Aussagen führt wie die vorgestellte Theorie mit ihren ebenen Wahrscheinlichkeitswellen, werden genauere Daten das aufklären. Als bedeutende Bestätigung der Wellentheorie (MQT) sehe ich allerdings eine der ersten Aufnahmen der ca. 450 Lichtjahre entfernten Protostellaren Staubscheibe HL-Tauri, die am ALMA-Observatorium in der chilenischen Atacamawüste gelungen ist.
Die Abbildungen zeigen die Staubscheibe HL_Tauri und einen Größenvergleich mit unserem Sonnensystem. Deutlich sind Strukturen zu erkennen, die sehr den theoretischen Wellendarstellungen der von mir vorgestellten Theorie ähneln. Anders als die Interpretation der Astronomie gehe ich jedoch davon aus, dass Planeten sich nicht in den "Gaps" entwickeln, sondern hier direkt die Wellen der Wahrscheinlichkeitsdichte auch die Verteilung der Materie prägt. Meine Begründung ist, dass je mehr Materie sich an Orten befindet, es um so heller in der Darstellung ist, denn am hellsten ist es im Zentrum der Staubscheibe HL-Tauri, wo sich der Stern bildet, der seine Fusion noch nicht (vollständig) gezündet hat, denn es ist kein durch den Strahlungsdruck ausgelöstes "Wegblasen" zu erkennen. Planeten sollten sich jedoch dort bilden, wo am meisten Materie vorhanden ist. Auf den Bildern ist auch eine Winkelabhängigkeit der Materie zu erkennen, was eigentlich bei der Art meiner Gleichungen auch zu erwarten ist, obwohl ich bisher selbst nur die radiale Komponente untersucht habe.
Die Gleichungen sind aus der klassischen Mechanik (Keplergesetze, Hamilton-Formalismus) hergeleitet.

bzw.


bzw.


Eine Frage, die mich lange beschäftigt hat. Sicher ist, schon Kepler hat versucht, die mittleren Planetenbahnabstände - er hatte nur Werte von sechs Planeten - in eine weitere vierte Regel zu packen, denn er glaubte an die Harmonie der Schöpfung. Die mittleren Bahnabstände muss er schon recht genau gekannt haben, sonst wären ihm die zweite und dritte Keplersche Regel nicht gelungen, die letztere veröffentlichte er erst 10 Jahre (1619) nach den anderen zwei.
Platonische Körper sollten zur Lösung verhelfen.
Wir wissen, sie halfen nicht.


Auch als Newton 1687 sein Gravitationsgesetz bekannt machte und damit die drei Keplerschen Regeln zu physikalischen Gesetzen adelte, führte nichts zur Erklärung der Bahnabstände. Mehrfach wurde die Lösung in der Folgezeit versucht, oben habe ich als Beispiel die Titius-Bode-Reihe erwähnt (Titius 1766, Bode 1772 und schließlich Wurm 1787 mit Einführung der Astronomischen Einheit (AE)), aber alles vergeblich.
Selbst Einsteins Allgemeine Relativitätstheorie (ART), die als umfassende Beschreibung der Gravitation gilt, lieferte keinerlei Hinweise, die auf eine physikalische Erklärung der Bahndaten hindeuteten. Was Wunder, dass die Ansicht namhafter Physiker schließlich dahin driftete, es gäbe gar keine Systematik oder physikalischen Grund, alles sei nur historischer Zufall.
Mich selbst habe ich gefragt, warum auch ich mehrere Jahrzehnte erfolglos nach einer Lösung gesucht habe, selbst dann noch, als es mir 1981/82 nach vielen Jahren vergeblichen Suchens gelungen war, die am Anfang gezeigten Gleichungen mathematisch mit Überlegungen aus der klassischen Mechanik herzuleiten. Gleichungen, die wie ich heute weiß, sehr wohl die Lösungen enthielten.
Meine Gleichungen lieferten nicht nur die Lösung, sondern beantworteten auch diese Frage. Eigentlich hätte ich es mit gründlichen Überlegungen eher herausfinden können! Die Suche nach einer Systematik der mittleren Entfernungen ist unsinnig. Die mittlere Entfernung einer elliptischen Bahn ist für die Bahnentfernung ohne Belang, sie ist nur der Mittelwert der beiden Apsidenentfernungen! Ist nur eine Abstraktion, denn dort hält sich ein Himmelskörper radial gesehen nur kurze Zeit auf, am längsten verweilt er in der Entfernung der Apsiden, denn da hat die radiale Impulskomponente seines Umlaufs ein Minimum.
Auch hat die mittlere Entfernung keinerlei Bezug zur Bahnexzentrizität, nur die Apsiden bestimmen die Exzentrizität einer Ellipse.
Exzentrische Bahnen aber sind keineswegs die Ausnahme, bei den inneren Planeten haben Merkur und Mars deutliche Abweichungen von der Kreisbahn und auch die äußeren Planeten haben beachtliche Apsidendifferenzen. Den beeindruckendsten Wert liefert Pluto, e = 0.2488 ~ 0.25 = (5.-3.)/(5.+3.)Maximum der zu ihm und den großen Planeten gehörenden Welle der Wahrscheinlichkeitsdichte.
Letzteres ist auch der Grund, weshalb Pluto für mich ein "ordentlicher", wenn auch sehr kleiner Planet bleibt. Hat nicht die ART gezeigt, dass Objekte in einem Gravitationsfeld sich auf Geodäten bewegen, also stets einer kräftefreien Bewegung folgen?
Wo aber keine Kraft wirkt, spielt auch die Masse keine Rolle! Und ich frage mich, wieso klassifiziert man Planeten nach ihrer Größe?
Übrigens, schon Galilei wusste, dass Körper unabhängig von ihrer Masse gleich schnell fallen.